Перетворювач прямого коду в доповняльний код

Таблиця 3.14. Перетворення прямого коду в обернений.

X	Y
ХЗ Н =0	Х ЗН =1
Х 0
Х 1
Х 2
Х 3

Схему п’ятирозрядного перетворювача прямого коду в обернений, побудовану на елементах "Виключальне АБО" відповідно виразу (3.25), показано на рис. 3.20.

Рис. 3.20. Перетворювач прямого коду в обернений: а – схема; б – часова діаграма роботи.

В процесі перетворення прямого коду в обернений значення знакового розряду Х_зн використовується як керуючий сигнал, який забезпечує отримання наступного виразу:

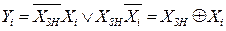
де Y_i – значення i-го розряду оберненого коду;

X_i – значення i-го розряду додатнього вхідного числа (X_ЗН = 0);

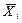–значення i- го розряду відє'много вхідного числа (= 1).

Доповняльний код додатного двійкового числа збігається з його прямим і оберненим кодами. Доповняльний код від'ємного двійкового числа утворюється з його оберненого коду додаванням до молодшого розряду одиниці. Таким чином, операція перетворення прямого коду в доповняльний код не є порозрядною і виконується значно складніше, ніж отримання оберненого коду.

Таблиця 3.15. Відповідність між прямим і доповняльним кодами

Прямий код

Доповняльний код

Прямий код

Доповняльний код

Х4

X3

Х2

Х1

Y4

Y3

Y2

Y1

X4

X3

Х2

X1

Y4

Y3

Y2

Y1

Відповідність між прямим і доповняльним кодами на прикладі чотирьох цифрових розрядів представлено в табл. 3.15.

Знаковий розряд прямого коду використовується як управляючий сигнал: якщо X _ЗН = 0, то вихідний код повторює значення вхідного; при Х _ЗН = 1 реалізується перетворення згідно табл. 3.15.

Карту Карно, відповідну табл. 3.15 для отримання мінімальних форм функцій перетворення прямого коду в доповняльний, представлено на рис. 3.21.

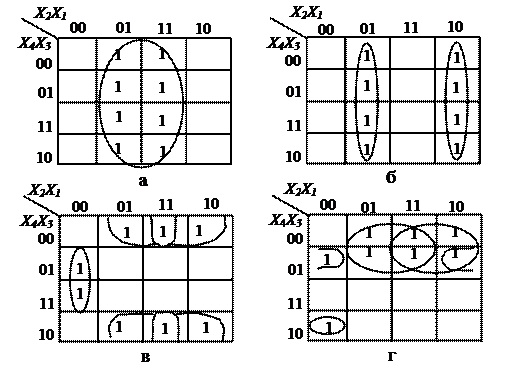Рис. 3.21. Карта Карно для функцій перетворювача прямого коду в доповняльний код: а – Y₁; б – Y₂; в – Y₃; г – Y₄

На основі карт Карно з урахуванням знакового розряду Х_ЗН прямого коду для функцій Y ₁ Y ₂ Y ₃ Y ₄, що представляють виходи перетворювача, отримуємо:

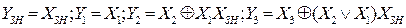
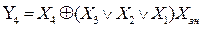
Схему перетворювача прямого коду в доповняльний код на основі виразів показано на рис. 3.22.

Даний перетворювач характеризується високою швидкодією. Час встановлення вихідного коду визначається трьома затримками поширення сигналу, проте зі зростанням номера розряду лінійно зростає і необхідне число входів елементів АБО, що використовуються у схемі.

Рис. 3.22. Перетворювач прямого коду в доповняльний: а – схема, б – часові діаграми роботи.

Дата добавления: 2013-12-14