Перетворювач прямого коду в код Грея

Код Грея утворюється послідовністю двійкових чисел, в яких два будь-яких сусідніх числа відрізняються тільки одним розрядом (таблиця 3.16). Перше і останнє число вважаються сусідніми. Код Грея, який називають циклічним, відноситься до незважених двійкових кодів.

До переваг коду Грея відносять: зручність кодування кутових переміщень, простота кодуючої логіки, скорочення часу перетворення у зв'язку із зміною значення тільки одного розряду, висока ефективність захисту від збоїв. Недоліками коду Грея є ускладнення при виконанні арифметичних операцій і цифро-аналогових перетворень. Тому при необхідності код Грея перетворюють в двійковий код.

Таблиця 3.16. Утворення коду Грея послідовністю двійкових чисел

X4

X3

X2

X1

I4

I3

I2

I1

X4

X3

X2

X1

I4

I3

I2

I1

За даними таблиці 3.16 у клітинки карт Карно (рис. 3.23) внесені значення розрядів I₁ I₂, I₃, I₄ коду Грея.

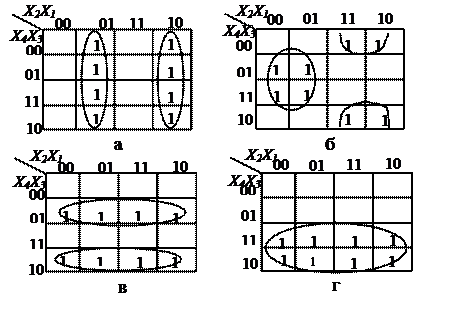Рис. 3.23. Карта Карно для кодів Грея: а — I₁, б —I₂, в —I₃, г — I₄

Схему перетворювача прямого коду в код Грея показано на рис. 3.24.

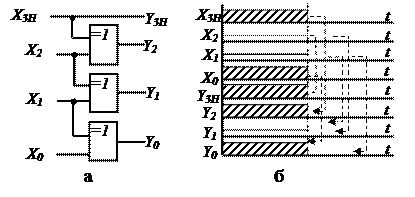Рис. 3.24. Перетворювач прямого коду в код Грея: а – схема, в – часова діаграма роботи.

За допомогою карт Карно отримуємо наступні вирази для розрядів коду Грея:

;

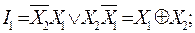
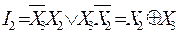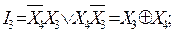
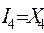
Схема та часова діаграма роботи перетворювача коду Грея в прямий код наведені на рис. 3.25.

Рис. 3.25. Перетворювач кода Грея в прямий код: а – схема, б – часова діаграма роботи.

4.4 Двійкові суматори

4.4.1 Загальна характеристика суматорів

Функціональний вузол комп'ютера, призначений для додавання двох n -розряднихслів (чисел) називається суматором.

Операція віднімання замінюється додаванням слів в оберненому або доповняльному коді. Операції множення і ділення зводяться до реалізації багатократних додаваннь та зсувів. Тому суматор є важливою частиною арифметико-логічного пристрою. Функція суматора позначається буквами SМ або ∑.

Окремі схеми, із яких складається суматор, називаються однорозрядними суматорами. Вони виконують усі дії з додавання значень однойменних розрядів двох чисел (операндів). Суматори класифікуються за такими ознаками:

· спосіб додавання – паралельні, послідовні і паралельно-послідовні;

· число входів – напівсуматори, однорозрядні і багаторозрядні суматори;

· організація зберігання результату додавання – комбінаційні, накопичувальні, комбіновані;

· організація перенесення між розрядами – з послідовним, наскрізним, паралельним або комбінованим перенесенням (з груповою структурою);

· система числення – позиційні (двійкові, двійково-десяткові, трійкові) і непозиційні, наприклад, в системі залишкових класів;

· розрядність (довжина) операндів – 8-, 16-, 32-, 64-розрядні;

· спосіб представлення від'ємних чисел – в оберненому або доповняльному кодах, а також в їхніх модифікаціях;

· час додавання – синхронні, асинхронні.

У паралельних n-розрядних суматорах значення всіх розрядів операндів поступають одночасно на відповідні входи однорозрядних підсумовувальних схем. У послідовних суматорах значення розрядів операндів та перенесення, що запам'ятовувалося в попередньому такті, поступають послідовно в напрямку від молодших розрядів до старших на входи одного однорозрядного суматора.

У паралельно-послідовних суматорах числа розбиваються на частини, наприклад, байти, розряди байтів поступають на входи восьмирозрядного суматора паралельно (одночасно), а самі байти – послідовно, в напрямку від молодших до старших байтів з урахуванням попереднього перенесення.

У комбінаційних суматорах результат операції додавання запам'ятовується в регістрі результату. У накопичуючих суматорах процес додавання об'єднується із зберіганням результату. Це пояснюється використанням T -триггерів як однорозрядних схем додавання.

Організація перенесення практично визначає час виконання операції додавання. Послідовні перенесення схем утворюються просто, проте є повільно діючими. Паралельні перенесення схемно організовуються значно складніше, проте дають високу швидкодію.

Розрядність суматорів знаходиться в широких межах: 4-16 - для мікро- і міні-комп'ютерів і 32-64 і більше – для універсальних машин.

Синхронними є суматори з постійним інтервалом часу для додавання. Суматори, в яких інтервал часу для додавання визначається моментом фактичного закінчення операції, називаються асинхронними.

В асинхронних суматорах є спеціальні схеми, які визначають фактичний момент закінчення додавання і повідомляють про це в пристрій управління. На практиці використовують переважно синхронні суматори.

Суматори характеризуються наступними параметрами:

· швидкодією – часом виконання операції додавання t_∑, який відраховується від початку подачі операндів до отримання результату; часто швидкодія характеризується кількістю додавань за секунду F_∑ = 1/t_∑, маючи на увазі операції типу регістр-регістр (тобто числа зберігаються в регістрах АЛП);

· апаратними витратами: вартість однорозрядної схеми додавання визначається загальним числом логічних входів елементів, що використовуються; вартість багаторозрядного суматора визначається загальною кількістю мікросхем; споживаною потужністю суматора.

4.4.2 Однорозрядні суматори

Логічна схема, яка виконує додавання значень i-х розрядів Х_i і Y_i двійкових чисел з урахуванням перенесення Z_i з молодшого сусіднього розряду і виробляє на виходах функції результат S_i і перенесення P_i в старший сусідній розряд називається однорозрядним суматором. На основі однорозрядних схем додавання на три входи і два виходи будуються багаторозрядні суматори будь-якого типу. Алгоритм роботи однорозрядного суматора відображається таблицею істинності (табл. 3.20).

Таблиця 3.20. Алгоритм роботи однорозрядного суматора.

X i	Y i	Z i	S i	P i

На основі таблиці 3.20 записується система логічних функцій для результату S_i і перенесення Р_i:

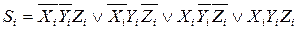
Мінімізацію функцій за допомогою карт Карно показано на рис. 3.30.

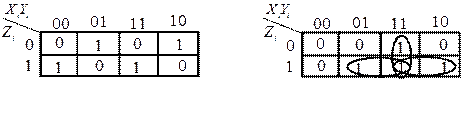
Рис. 3.30. Карти Карно для мінімізації функцій: а – S_i; б – P_i

Як видно з карт Карно, функція результату S_i не мінімізується, а функція Р_i мінімізується з пониженням рангу кон'юнкції і використовує тільки прямі значення змінних:

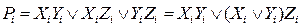
При проектуванні комбінаційних однорозрядних суматорів враховують наступні чинники:

· схема повинна характеризуватися регулярністю (подібністю) структури і мінімальною вартістю;

· з метою підвищення швидкодії багаторозрядного суматора потрібний мінімальний час отримання функції перенесення;

· t _П = кt _Р, де к – число послідовно включених елементів від входів до виходів P_i або 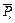; t_Р – середня затримка розповсюдження сигналу одним логічним елементом у вибраній серії інтегральних мікросхем; параметр часто називають каскадністю (поверховістю) схем, таким чином, для мінімізації часу отримання перенесення необхідно зменшити каскадність схеми і використовувати інтегральні мікросхеми з малим часом затримки розповсюдження сигналу;

· для схем однорозрядних суматорів на основі рівнянь необхідно виробляти як прямі P_i, так і інверсні 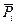значення функції перенесення, яку називають парафазною.

Рівняння (3.31) і (3.32) можуть бути виражені через функцію "Виключальне АБО ":

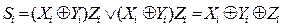
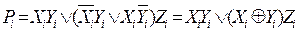
Схему однорозрядного суматора на елементах "Виключальне АБО" показано на малюнку 3.23б. Її вартість складає вісім входів, каскадність к дорівнює 2.

Логічна схема, яка виконує додавання значень i -хрозрядів Х_i і Y_i двійкових чисел Х і Y і реалізує на виході значення результату М_i і перенесення в старший сусідній розряд R_i називається напівсуматором:

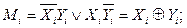
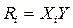
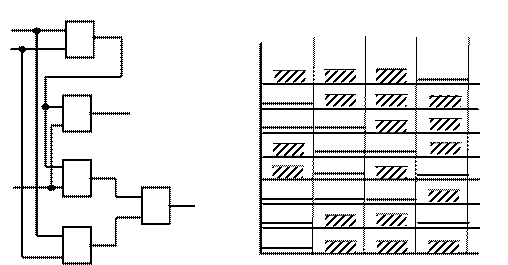а б

Рис. 3.31. Однорозрядний суматор з використанням власного перенесення: а – схема, б – часова діаграма роботи

Таким чином, напівсуматор виконує лише частину завдання підсумовування в i -мрозряді, оскільки не враховує перенесення з сусіднього молодшого розряду.

Контрольні запитання

1. Що називають перетворювачами кодів?

2. Які коди використовують для представлення інформації?

3. Що забезпечується за допомогою кодів?

4. Для чого відводиться знаковий розряд числа?

5. Перетворення прямого коду в обернений.

6. Схема і принцип дії перетворювача прямого коду в обернений.

7. Часова діаграма роботи перетворювача прямого коду в обернений.

8. Утворення доповняльного коду.

9. Схема і принцип дії перетворювачів прямого коду в доповняльний.

10. Часова діаграма роботи перетворювачів прямого коду в доповняльний.

11. Утворення і переваги коду Грея.

12. Схема і принцип дії перетворювача двійкох чисел в код Грея.

13. Часова діаграма роботи перетворювача двійкових чисел в код Грея.

14. Обернене перетворення кода Грея.

15. Схема і принцип дії перетворювача коду Грея в прямий код.

16. Часова діаграма роботи перетворювача коду Грея в прямий код.

17. Що називають суматором?

18. Класифікація суматорів.

19. Що називають послідовним суматором?

20. Що називають паралельним суматором?

21. В яких кодах додають від′ємні числа?

22. Що називають однорозрядним суматором?

23. Алгоритм роботи однорозрядного суматора.

24. Навести схему й описання принцип роботи однорозрядного суматора.

Дата добавления: 2013-12-14