Основні поняття

Зміст лекції

Психометричні основи психодіагностики: основні етапи конструювання тесту.

Означення: Функція називається неперервною в точці х = а, якщо:

1) вона визначена в цій точці;

2) існує ;

3) ця границя дорівнює значенню функції в точці х = а, тобто

.

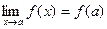Означення: Функцію 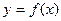називають неперервною на проміжку , якщо вона

неперервна в кожній точці цього проміжку.

Означення: Функцію 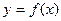називають неперервною в точці 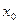справа, якщо

.

Означення: Функцію 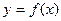називають неперервною в точці 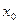зліва, якщо

.

Означення: Якщо хоча б одна з умов неперервності функції в точці порушується, то таку точку 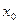називають точкою розриву функції .

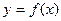2. Класифікація точок розриву функцій

Означення. Функція 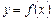називається розривною в точці якщо порушується хоча б одна з умов рівності

Розрізняють точки розриву 1-го і 2-го роду. Розриви 1-го роду бувають усувні й неусувні; розриви 2-го роду — завжди неусувні.

Означення. Точка 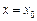називається точкою розриву 2-го роду для функції 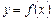, якщо в цій точці не існує хоча б одна з односторонніх границь (зліва чи справа).

Означення. Точка 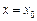називається точкою розриву 1-го роду (розрив неусувний) для функції 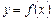, якщо односторонні границі (зліва і справа) функції у цій точці існують, але не рівні між собою, тобто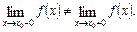

Означення. Точка 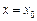називається точкою розриву 1-го роду (розрив усувний) для функції 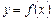, якщо односторонні границі функції в цій точці існують, рівні між собою, але не дорів­нюють значенню функції в цій точці або функція у цій точці не існує, тобто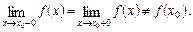

Зауваження. Точка 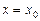усувного розриву відзначається тим, що існує 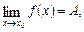але 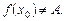Тому на основі функції 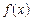можна побудувати функцію

3. Властивості неперервних функцій

Теорема: Якщо функції 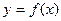та неперервні в точці 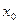, то функції , , 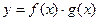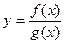(при ) також неперервні в цій точці.

4. Властивості функцій неперервних на відрізку (подані у вигляді теорем):

Теорема 1 (Вейєрштрасса): Якщо функція неперервна на відрізку , то вона

обмежена на цьому відрізку.

Теорема 2 (Вейєрштрасса): Неперервна на відрізку функція 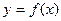досягає на

ньому свого найбільшого та найменшого значень, тобто існують точки 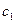та такі, що , причому

Теорема (Больцано-Коші): Якщо функція 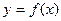неперервна на відрізку і набуває

на кінцях відрізка значень різних знаків, тобто 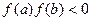, то всередині відрізка існує принаймні одна точка така, що f (с) = 0.

5.Методика дослідження функцій на неперервність.

1. Знайти область визначення функції

2. Дослідити функцію на неперервність у відкритих проміжках

3. Визначити скінченні граничні точки (с.г.т.) і обчислити односторонні границі функції у цих точках.

Рис. 1

4. Зробити висновок про характер точок розриву (якщо вони є) і побудувати графік функції поблизу цих точок. Для зручності побудови графіка функції рекомендується записати координати граничних точок графіка функції 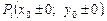Символічний запис абсциси граничної точки 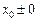означає, що абсциса довіль­ної точки графіка функції прямує до х ₀ зліва (х ₀ – 0) або справа (х ₀ + 0); а запис означає, що ордината довільної точки графіка функції при цьому прямує до у ₀ знизу (у ₀ – 0) або зверху (у ₀ + 0). Наприклад, для граничних точок і графік функції підходить до цих точок так, як показано на рис. 1.

До точки Р ₁ графік підходить зліва і зверху, а до точки Р ₂ — справа і знизу.

Приклад. Дослідити на неперервність функцію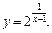

l Область визначення цієї функції 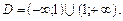На кож­ному з інтервалів області визначення функція буде неперервна, як суперпозиція неперервних елементарних функцій. Скінченною граничною точкою D функції буде х = 1. Обчислимо такі границі:

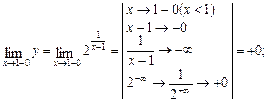
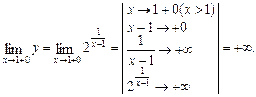
Отже, х = 1 — точка розриву 2-го роду, бо одна з односторонніх границь не існує. Граничні точки графіка функції: Р ₁ (1 – 0; + 0), Р ₂(1 + 0; + ¥). Графік функції поблизу точки розриву показано на рис. 2. Зауважимо, що гранична точка Р ₂ (1 + 0; + ¥) лежить на нескінченності.

Рис. 2 Рис. 3

Приклад. Дослідити на неперервність функцію

l Ця функція буде неперервною на кожному з проміжків
(–¥; 0) і (0; + ¥), бо є суперпозицією неперервних елементарних функцій. Границі — не існують. Отже, точка х = 0 — точка розриву функції 2-го роду.

Записати координати граничних точок графіка функції неможливо, тому і побудувати графік функції 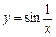поблизу самої точки розриву не можна (рис. 3).

Приклад. Дослідити на неперервність функцію .

l Скорочений запис розв’язування задачі:

— неперервна, як суперпозиція елементарних функцій.

х = 0 — с.г.т. D (y).

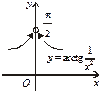Рис. 4

Таким чином, точка х = 0 є точкою розриву функції 1-го роду (розрив усувний), бо односторонні границі існують і рівні між собою (сама функція при х = 0 не існує).

Граничні точки графіка функці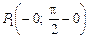ї і 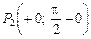зливаються в одну точку (рис. 4).

Приклад. Дослідити на неперервність функцію

l Після розкриття 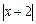функція перепишеться так:

На кожному з інтервалів 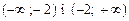функція неперервна. Розглянемо односторонні границі функції у точці х = – 2.

Рис. 5

Отже, точка х = – 2 — точка розриву 1-го роду (розрив неусувний), бо од­носторонні границі функції у цій точці існують, але не рівні між собою.

Граничні точки графіка функції такі: 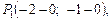(рис. 5).

Інший виклад за підручником Грисенко:

Дата добавления: 2013-12-14