
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Властивості бінарних відношень
|
|
|
|
Розглянемо спеціальні властивості бінарних відношень, що широко використовуються при побудові та дослідженні відношень переваги.
Рефлексивність. Бінарне відношення R називається рефлексивним, якщо справедливо 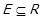 . Очевидно, що в цьому разі також
. Очевидно, що в цьому разі також 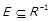 . Таким чином, рефлексивне відношення виконується для однакових елементів, тобто
. Таким чином, рефлексивне відношення виконується для однакових елементів, тобто 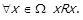 Введемо предикат
Введемо предикат 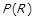 від бінарного відношення, який істинний тоді і лише тоді, коли R – рефлексивне.
від бінарного відношення, який істинний тоді і лише тоді, коли R – рефлексивне.
Антирефлексивність. Ця властивість є протилежною до рефлексивності. Відношення R називається антирефлексивним, якщо жодний елемент не знаходиться в цьому відношенні сам із собою, тобто 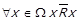 . Через операцію перетину це можна записати як
. Через операцію перетину це можна записати як 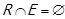 , а через включення – як
, а через включення – як 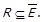 Також подібно до попередньої властивості введемо предикат антирефлексивності
Також подібно до попередньої властивості введемо предикат антирефлексивності 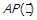 .
.
Симетричність. Відношення R є симетричним, якщо разом із кожною впорядкованою парою, що належить відношенню, воно містить і пару із переставленими компонентами, тобто 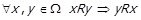 . Інакше це можна виразити як
. Інакше це можна виразити як 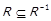 . Відповідний предикат будемо позначати
. Відповідний предикат будемо позначати 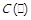 . Легко показати, що
. Легко показати, що 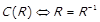 .
.
Асиметричність. Для асиметричного відношення R виконується 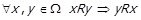 , тобто щонайбільше одна пара з
, тобто щонайбільше одна пара з 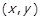 та
та 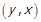 належить такому відношенню. Через операцію перетину це можна записати як
належить такому відношенню. Через операцію перетину це можна записати як 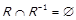 . Предикат асиметричності позначатимемо
. Предикат асиметричності позначатимемо 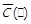 .
.
Антисиметричність. Відношення R називається антисиметричним, якщо 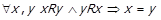 , тобто такому відношенню належать щонайбільше одна пара із різними компонентами з
, тобто такому відношенню належать щонайбільше одна пара із різними компонентами з 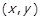 та
та 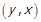 , та, можливо, пари однакових елементів. За допомогою операцій над відношеннями це можна записати як
, та, можливо, пари однакових елементів. За допомогою операцій над відношеннями це можна записати як 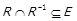 . Предикат антисиметричності отримує позначення
. Предикат антисиметричності отримує позначення 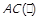 .
.
Відношення 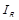 називається симетричною частиною вихідного відношення R, якщо
називається симетричною частиною вихідного відношення R, якщо 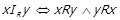 . Це симетричне відношення
. Це симетричне відношення 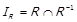 .
.
Відношення 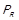 називається асиметричною частиною вихідного відношення R, якщо
називається асиметричною частиною вихідного відношення R, якщо 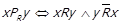 . Можна легко показати, що
. Можна легко показати, що 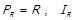 , тобто
, тобто
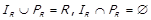 .
.
Відмітимо, що це означає, що 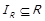 та
та 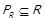 .
. 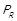 в загальному випадку асиметричне відношення.
в загальному випадку асиметричне відношення.
Транзитивність. Відношення R буде транзитивним, якщо кожний направлений шлях довжиною 2 в його графі замикається дугою, тобто 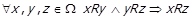 . Можна легко показати, що в графі транзитивного відношення дугою замикається направлений шлях будь-якої довжини, тобто
. Можна легко показати, що в графі транзитивного відношення дугою замикається направлений шлях будь-якої довжини, тобто
 .
.
Для транзитивного відношення виконується
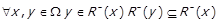 ,
,
тобто нижній переріз кожного елементу множини 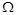 є максимальним за включенням серед нижніх перерізів елементів, яких він містить. Через операцію включення властивість транзитивності можна записати як
є максимальним за включенням серед нижніх перерізів елементів, яких він містить. Через операцію включення властивість транзитивності можна записати як 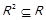 . Предикат транзитивності – це
. Предикат транзитивності – це 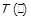 .
.
Лема 1.2. Для того, щоб R було транзитивним відношенням (щоб виконувалось 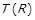 ) необхідно і достатньо справедливості
) необхідно і достатньо справедливості 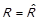 .
.
Доведення. ⇒ Доведемо за індукцією включення 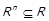 .
.
База: n = 2. 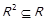 виконується за
виконується за 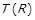 .
.
Припущення: 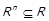 виконується для деякого
виконується для деякого 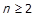 .
.
Перехід: 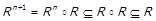 , і включення доведено
, і включення доведено 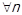 .
.
За означенням транзитивного замикання
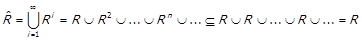 ,
,
тобто 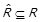 . Але зворотне включення
. Але зворотне включення 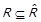 також тривіально виконується, тобто
також тривіально виконується, тобто 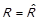 і необхідність доведена.
і необхідність доведена.
⇐ З означення транзитивного замикання очевидно 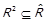 . Оскільки
. Оскільки 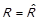 , то
, то 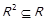 , тобто
, тобто 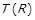 – достатність доведена.
– достатність доведена.
Доведено.
Від’ємна транзитивність. Відношення R називається від’ємно транзитивним, якщо транзитивним є його доповнення 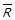 , тобто якщо
, тобто якщо 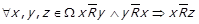 . Для від’ємної транзитивності введемо предикат
. Для від’ємної транзитивності введемо предикат 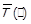 .
.
Лема 1.3. Для 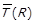 необхідно і достатньо справедливості твердження
необхідно і достатньо справедливості твердження
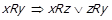 .
.
Доведення. ⇒ Нехай 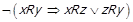 , тобто при
, тобто при 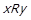 виконується
виконується 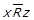 та
та 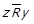 . Але з
. Але з 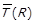
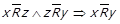 . Отримали протиріччя, яке доводить необхідність.
. Отримали протиріччя, яке доводить необхідність.
⇐ Нехай 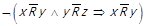 , тобто при
, тобто при 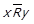 та
та 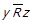 виконується
виконується 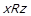 . Але, поклавши в
. Але, поклавши в 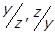 , маємо
, маємо 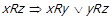 . Кожний з цих варіантів протирічить вихідному припущенню, і таким чином достатність твердження для від’ємної транзитивності також доведена.
. Кожний з цих варіантів протирічить вихідному припущенню, і таким чином достатність твердження для від’ємної транзитивності також доведена.
Доведено.
Зв’язність. Відношення R називається зв’язним, якщо виконується 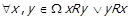 . Предикат, введений для властивості зв’язності, позначається
. Предикат, введений для властивості зв’язності, позначається 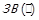 . Інша назва цієї властивості – лінійність. Зрозуміло, що зв’язне відношення обов’язково має бути рефлексивним. Граф
. Інша назва цієї властивості – лінійність. Зрозуміло, що зв’язне відношення обов’язково має бути рефлексивним. Граф 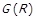 зв’язного відношення містить єдину компоненту зв’язності та петлі у кожній вершині.
зв’язного відношення містить єдину компоненту зв’язності та петлі у кожній вершині.
Слабка зв’язність. Будемо називати бінарне відношення R слабкозв’язним (відповідний предикат - 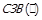 ), якщо
), якщо 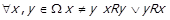 . Граф
. Граф 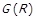 такого відношення, подібно до зв’язного, містить єдину компоненту зв’язності. Слабкозв’язне відношення не обов’язково має бути рефлексивним, тобто його граф може мати вершини, у яких відсутні петлі.
такого відношення, подібно до зв’язного, містить єдину компоненту зв’язності. Слабкозв’язне відношення не обов’язково має бути рефлексивним, тобто його граф може мати вершини, у яких відсутні петлі.
Не будь-який зв’язний граф відповідає слабкозв’язному відношенню, прикладом чому може слугувати дерево.
Теорема 1.1 (про взаємозв’язок властивостей бінарних відношень).
Мають місце наступні залежності між властивостями деякого бінарного відношення 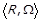 :
:
1) 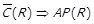 ; 2)
; 2) 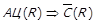 ; 3)
; 3) 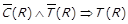 ;
;
4)  ; 5)
; 5) 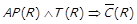 ; 6)
; 6) 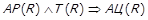 .
.
Доведення.
1) Нехай 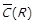 , тоді
, тоді 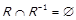 . Припустимо, що
. Припустимо, що 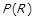 , тобто
, тобто 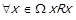 , тоді
, тоді 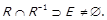
2) Нехай 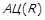 . Якщо при цьому
. Якщо при цьому 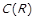 , то
, то 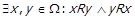 , тобто граф відношення R містить цикл довжини 2. Якщо ж
, тобто граф відношення R містить цикл довжини 2. Якщо ж 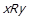 виконується лише коли
виконується лише коли 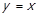 , то граф відношення містить петлю. Обидва ці випадки протирічать
, то граф відношення містить петлю. Обидва ці випадки протирічать 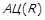 .
.
3) Нехай 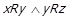 для деяких
для деяких 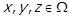 . За для
. За для 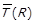 виконується
виконується 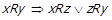 . За
. За 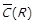
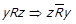 , тобто можливий лише випадок
, тобто можливий лише випадок 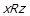 . Отримали
. Отримали  , звідки
, звідки 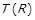 .
.
4) Нехай 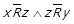 , але всупереч
, але всупереч 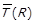
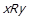 для деяких
для деяких 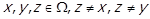 . Через те, що
. Через те, що 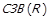 ,
, 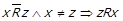 та
та 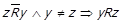 . Тобто
. Тобто  ,
, 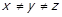 , що протирічить
, що протирічить 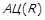 .
.
5) Нехай 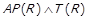 , але
, але 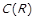 , тобто
, тобто 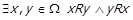 . За
. За 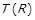
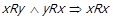 , що неможливо через
, що неможливо через 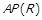 .
.
6) Нехай знову 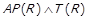 , але всупереч
, але всупереч 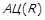
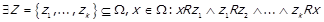 ,
,
тоді за 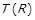
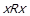 , чого не може бути згідно з
, чого не може бути згідно з 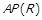 .
.
Доведено.
Для теореми 1.1 можна навести ряд наслідків, наприклад:
· 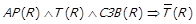 ;
;
· 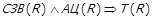 .
.
Відомості про взаємозв’язок властивостей бінарних відношень зручно представляти в табличному вигляді, рядок якої відповідає одному такому твердженню, стовпчик – окремій властивості. У комірці таблиці ставляться символи: ×, якщо антецедент твердження вимагає виконання відповідної властивості, та 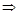 , який відмічає консеквент твердження. Викладені вище відомості зведені у табл. 1.1.
, який відмічає консеквент твердження. Викладені вище відомості зведені у табл. 1.1.
| Таблиця 1.1. –Відомості про взаємозв’язок властивостей бінарних відношень | ||||||
| № | 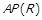
| 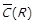
| 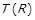
| 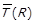
| 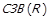
| 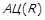
|
| ⇒ | × | |||||
| ⇒ | × | |||||
| × | ⇒ | × | ||||
| ⇒ | × | × | ||||
| × | ⇒ | × | ||||
| × | × | ⇒ | ||||
| Н1 | × | × | ⇒ | × | ||
| Н2 | ⇒ | × | × |
Розглянемо питання про інваріантність деяких властивостей бінарних відношень відносно операцій над ними. Наведемо відповідну теорему.
Теорема 1.2 (про інваріантність властивостей відношень відносно операцій між ними).
Для заданих бінарних відношень 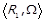 ,
, 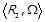 та будь-якого
та будь-якого 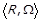 справедливі наступні твердження:
справедливі наступні твердження:
1) якщо 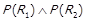 , то
, то  ,
, 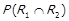 ,
, 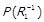 ,
, 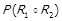 ,
, 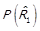 ;
;
2) якщо 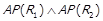 , то
, то 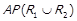 ,
, 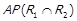 ,
, 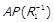 ;
;
3) якщо 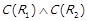 , то
, то 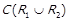 ,
, 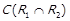 ,
, 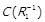 ,
, 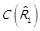 ;
;
4) якщо 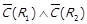 , то
, то 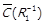 ,
, 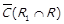 ;
;
5) якщо 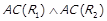 , то
, то 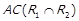 та
та 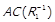 ;
;
6) якщо 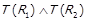 , то
, то 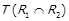 ,
, 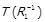 ,
, 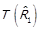 .
.
Доведення.
1) 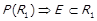 ,
, 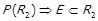 . З властивостей включення множин
. З властивостей включення множин
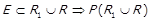 ,
,
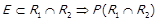 .
.
З 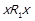 тривіальним чином випливає
тривіальним чином випливає 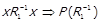 . Доведемо
. Доведемо 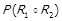 . З означення композиції відношень
. З означення композиції відношень 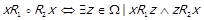 . В якості z також можна взяти елемент x. Тепер, беручи до уваги те, що
. В якості z також можна взяти елемент x. Тепер, беручи до уваги те, що 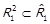 , вже доведене
, вже доведене 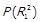 , та поклавши
, та поклавши 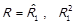 маємо
маємо
 .
.
2) Оскільки  , то за властивістю операції включення
, то за властивістю операції включення 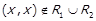 та
та 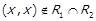 . Далі, з
. Далі, з 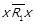 випливає
випливає 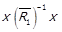 . За лемою 1.1 отримаємо
. За лемою 1.1 отримаємо
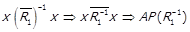 .
.
3) 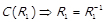 ,
, 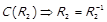 . Тоді за
. Тоді за
 ,
,
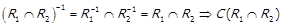 .
.
Подібним чином з інволютивності обернення 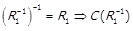 . З
. З
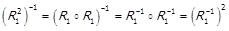 .
.
За індукцією 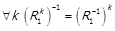 . Знову використавши отримаємо
. Знову використавши отримаємо
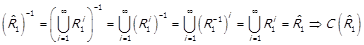 .
.
4) Відомо, що 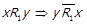 .
. 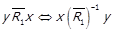 . За лемою 1.1 маємо
. За лемою 1.1 маємо 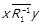 . Також
. Також 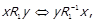 тобто
тобто
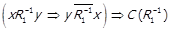 .
.
Тепер нехай для деяких 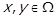
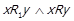 . Це зокрема означає, що
. Це зокрема означає, що  . Оскільки
. Оскільки 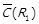 , має місце
, має місце
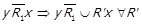 .
.
Візьмемо 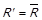 , використавши правило де Моргана отримаємо
, використавши правило де Моргана отримаємо
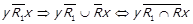 .
.
Звідси 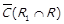 .
.
5) 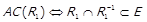 ,
, 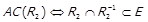 . Тоді
. Тоді
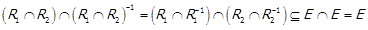 ,
,
отже 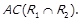 Подібним чином
Подібним чином
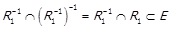 ,
,
і  .
.
6) Нехай справедливі співвідношення 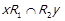 та
та 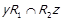 для деяких
для деяких 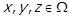 . Тоді також вірні
. Тоді також вірні 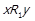 ,
, 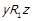 ,
, 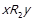 ,
, 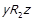 . За
. За 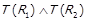 отримаємо
отримаємо 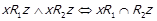 , і
, і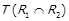 доведено. Якщо справджується
доведено. Якщо справджується 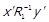 та
та  для деяких
для деяких 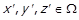 , то за визначенням оберненого відношення маємо
, то за визначенням оберненого відношення маємо 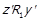 та
та 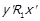 . За
. За 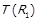 отримаємо
отримаємо 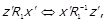 що доводить
що доводить 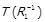 . Далі,
. Далі, 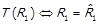 за лемою 1.2. Тоді
за лемою 1.2. Тоді 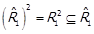 , звідки
, звідки 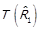 .
.
Доведено.
|
|
|
|
|
Дата добавления: 2013-12-14; Просмотров: 3569; Нарушение авторских прав?; Мы поможем в написании вашей работы!