
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Класифікація бінарних відношень
|
|
|
|
Розглянуті властивості та їхній взаємозв’язок дозволяють виділити та досліджувати окремі класи відношень, що є корисними при моделюванні переваг.
Еквівалентність. Рефлексивне, симетричне та транзитивне бінарне відношення R називається відношенням еквівалентності. Це записується як  .
.
Теорема 1.3. Якщо R – відношення еквівалентності (предикат 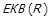 істинний), то
істинний), то 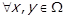 виконується
виконується  .
.
Доведення. Нехай для деяких 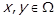
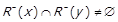 . Тоді
. Тоді  , і за означенням нижнього перерізу
, і за означенням нижнього перерізу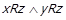 . Оскільки
. Оскільки  , має місце
, має місце  . За
. За 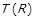
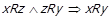 , та знову за
, та знову за 
 .
.
Нехай  , тобто має місце
, тобто має місце 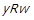 . За
. За 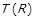
 , тобто
, тобто 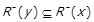 .
.
Доведемо зворотне включення. Нехай  . За
. За 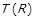
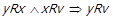 , і
, і 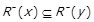 . Остаточно
. Остаточно  .
.
Доведено.
Сімейство непорожніх підмножин  множини Ω називається її розбиттям, якщо
множини Ω називається її розбиттям, якщо
1)  ;
;
2)  .
.
Самі підмножини  називаються класами розбиття. За домовленістю для подальшого викладення будемо вважати, що
називаються класами розбиття. За домовленістю для подальшого викладення будемо вважати, що  .
.
Примітка 1.1 (до теореми 1.3). Для відношення еквівалентності сімейство його нижніх перерізів для кожного елементу множини  є суть її розбиттям, тобто виконується
є суть її розбиттям, тобто виконується  .
.
Щодо існування розбиття для відношення еквівалентності має місце і зворотне твердження.
Теорема 1.4. Нехай на множині  задано деяке розбиття
задано деяке розбиття  . Введемо на
. Введемо на  відношення R виду
відношення R виду
 .
.
Тоді 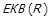 .
.
Доведення.  . Перевіряємо кожну із властивостей R.
. Перевіряємо кожну із властивостей R.
Нехай 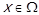 , тоді за означенням розбиття
, тоді за означенням розбиття  , тобто
, тобто 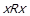 , звідки
, звідки  .
.
Нехай  , тобто
, тобто  для деякого
для деякого 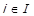 . Але порядок розгляду елементів множини
. Але порядок розгляду елементів множини  не важливий, отже
не важливий, отже 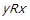 . Таким чином
. Таким чином  , а значить
, а значить  .
.
Нарешті, нехай  , тобто
, тобто  та
та  для деяких
для деяких  . Можливий лише один з двох випадків:
. Можливий лише один з двох випадків:  або
або  , оскільки
, оскільки  – розбиття
– розбиття  . Але перший випадок неможливий, оскільки
. Але перший випадок неможливий, оскільки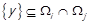 . Отже
. Отже  ,
,  . Отримали
. Отримали  , та істинність
, та істинність 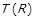 доведено.
доведено.
Доведено.
Примітка 1.2 (до теореми 1.4). Множини  називаються класами еквівалентності відношення R. Сімейство усіх класів еквівалентності відношення R називають фактор-множиною
називаються класами еквівалентності відношення R. Сімейство усіх класів еквівалентності відношення R називають фактор-множиною  по еквівалентності R, та позначають
по еквівалентності R, та позначають  . Вона визначається наступним чином
. Вона визначається наступним чином
 .
.
Із відношенням еквівалентності тісно пов’язане поняття факторизації.
Нехай задане деяке відношення 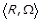 . Нехай до того ж на
. Нехай до того ж на  задане деяке відношення еквівалентності
задане деяке відношення еквівалентності 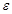 (для цього достатньо задати деяке розбиття
(для цього достатньо задати деяке розбиття  множини
множини  ). Побудуємо на фактор-множині
). Побудуємо на фактор-множині 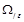 відношення
відношення 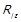 наступним чином:
наступним чином:
 .
.
Таким чином, пара класів еквівалентності знаходиться у відношенні 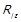 тоді і тільки тоді, коли знайдуться такі представники цих класів, які знаходяться у відношенні R.
тоді і тільки тоді, коли знайдуться такі представники цих класів, які знаходяться у відношенні R.
Операцію отримання 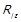 називають факторизацією відношення R за еквівалентністю
називають факторизацією відношення R за еквівалентністю 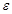 , а отримане відношення
, а отримане відношення 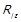 – фактор-відношенням. Подібним чином можна говорити про те, що відношення еквівалентності
– фактор-відношенням. Подібним чином можна говорити про те, що відношення еквівалентності 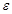 визначає факторизацію множини
визначає факторизацію множини  як операцію отримання по
як операцію отримання по 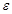 відповідної фактор-множини
відповідної фактор-множини 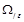 .
.
Розглянемо приклад факторизації. Нехай  , і на цій множині задано відношення R, граф
, і на цій множині задано відношення R, граф 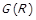 якого зображено на рис. 1.2. Також на
якого зображено на рис. 1.2. Також на  задано розбиття
задано розбиття
 .
.
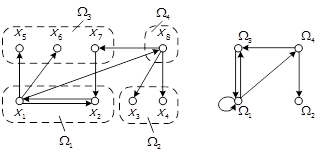
Рис. 1.2 – Графи відношення 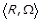 до прикладу здійснення операції факторизації та відповідного фактор-відношення
до прикладу здійснення операції факторизації та відповідного фактор-відношення 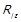
На рис. 1.2 класи еквівалентності відповідного відношення еквівалентності 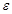 обведено пунктирною лінією. Також на цьому рисунку наведений граф фактор-відношення. При побудові фактор-відношення слід звернути уваги на можливі петлі, що виникають, коли у вихідному відношенні R існують пари, компоненти яких належать одному класу еквівалентності.
обведено пунктирною лінією. Також на цьому рисунку наведений граф фактор-відношення. При побудові фактор-відношення слід звернути уваги на можливі петлі, що виникають, коли у вихідному відношенні R існують пари, компоненти яких належать одному класу еквівалентності.
Тепер розглянемо питання про перехід спеціальних властивостей відношень на фактор-відношення. Будемо казати, що властивість 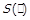 зберігається при факторизації, якщо
зберігається при факторизації, якщо  .
.
Теорема 1.5 (про інваріантність властивостей відношень відносно операції факторизації).
Для заданого бінарного відношення 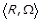 та відношення еквівалентності
та відношення еквівалентності 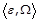 ,
, 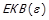 виконується:
виконується:
1) 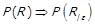 ; 2)
; 2) 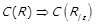 ;
;
3)  ; 4)
; 4) 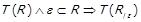 ;
;
5)  .
.
Доведення.
1) Нехай  – клас еквівалентності відношення
– клас еквівалентності відношення 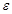 . Тоді
. Тоді  . Оскільки
. Оскільки  ,
, 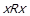 , і за визначенням фактор-відношення
, і за визначенням фактор-відношення 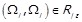 . Розглядаючи усі
. Розглядаючи усі  приходимо до висновку, що
приходимо до висновку, що  .
.
2) Нехай 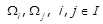 – класи еквівалентності відношення
– класи еквівалентності відношення 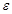 , та
, та  ,
, 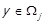 . Якщо
. Якщо  , то
, то  .
. 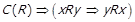 , тобто справджується
, тобто справджується 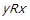 , звідки
, звідки  , і
, і  .
.
3) Нехай  . Тоді
. Тоді 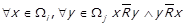 , що протирічить
, що протирічить  .
.
4) Візьмемо такі класи еквівалентності відношення 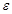
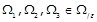 , що
, що  та
та 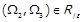 . Тоді для деяких елементів
. Тоді для деяких елементів 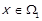 ,
, 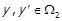 ,
,  виконується
виконується  ,
,  . Оскільки y та
. Оскільки y та 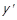 знаходяться в одному класі еквівалентності,
знаходяться в одному класі еквівалентності, 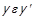 . Враховуючи те, що
. Враховуючи те, що 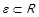 , маємо
, маємо 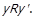 Отже
Отже  , за
, за 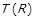 отримуємо
отримуємо  , що за визначенням фактор-відношення означає
, що за визначенням фактор-відношення означає  . Таким чином доведено
. Таким чином доведено 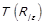 .
.
5) ⇒ Нехай виконується 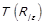 , тобто
, тобто 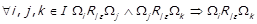 . Нехай
. Нехай 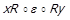 Це означає, що існує послідовність елементів
Це означає, що існує послідовність елементів  з множини
з множини  така, що
така, що  . З означень класів еквівалентності
. З означень класів еквівалентності 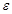 та фактор-відношення
та фактор-відношення 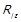 це означає, що
це означає, що
 .
.
З того, що 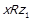 слідує
слідує  , а з
, а з 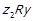 –
– 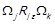 . За
. За 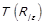 справедливе
справедливе 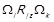 , тобто
, тобто
 .
.
Але тоді 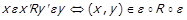 , тобто
, тобто 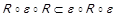 , і необхідність доведено.
, і необхідність доведено.
⇐ Припустимо тепер, що 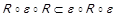 . Це означає, що знайдуться такі елементи
. Це означає, що знайдуться такі елементи  , що
, що 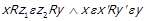 . Використовуючи означення класів еквівалентності
. Використовуючи означення класів еквівалентності 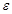 та фактор-відношення
та фактор-відношення 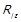 маємо
маємо
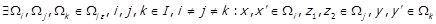 .
.
Але 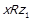 , тобто
, тобто  , та
, та 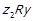 , тобто
, тобто 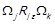 . Разом із цим,
. Разом із цим, 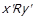 , тобто в цьому разі обов’язково має виконуватись
, тобто в цьому разі обов’язково має виконуватись 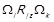 . Ми показали, що
. Ми показали, що 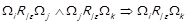 , з чого випливає
, з чого випливає 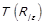 , і достатність також доведено.
, і достатність також доведено.
Доведено.
Примітка 1.3 (до теореми 1.5). В пункті 4 умова 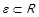 є суттєвою. В загальному випадку необхідною та достатньою умовою транзитивності фактор-відношення за довільною еквівалентністю
є суттєвою. В загальному випадку необхідною та достатньою умовою транзитивності фактор-відношення за довільною еквівалентністю 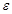 буде умова 5. Умова 4 є частковим випадком умови 5. Так, зокрема якщо
буде умова 5. Умова 4 є частковим випадком умови 5. Так, зокрема якщо  , та
, та 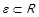 , маємо
, маємо
 .
.
Оскільки  , отримаємо
, отримаємо  , тобто
, тобто 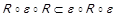 .
.
Зазначимо, що якщо відповідно відношенню еквівалентності 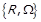 , що задає розбиття
, що задає розбиття  на
на  , визначити функціональне відображення
, визначити функціональне відображення 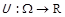 наступним чином:
наступним чином:
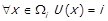 ,
,
то очевидно виконується 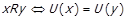 , а тому виконується також
, а тому виконується також 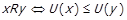 . Як буде видно далі,
. Як буде видно далі,  – рангова шкала еквівалентності R.
– рангова шкала еквівалентності R.
Строгий порядок. Антирефлексивне та транзитивне відношення називається відношенням строгого порядку. Інакше це означення можна записати як  . Очевидно, що через залежність властивостей бінарних відношень (теорема 1.1)
. Очевидно, що через залежність властивостей бінарних відношень (теорема 1.1) 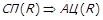 (граф строгого порядку ациклічний) та
(граф строгого порядку ациклічний) та 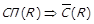 . Також слід зазначити, що оскільки
. Також слід зазначити, що оскільки 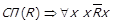 , строгий порядок не може бути зв’язним. Для строгого порядку можлива лише слабка зв’язність.
, строгий порядок не може бути зв’язним. Для строгого порядку можлива лише слабка зв’язність.
Елемент 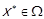 такий, що
такий, що  виконується
виконується  називається найбільшим елементом на множині
називається найбільшим елементом на множині  по відношенню R. Має місце наступне твердження.
по відношенню R. Має місце наступне твердження.
Лема 1.4. Нехай задано 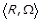 , і
, і 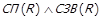 ,
, 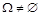 та
та  . Тоді існує єдиний найбільший по R елемент
. Тоді існує єдиний найбільший по R елемент  на
на  .
.
Доведення. Виберемо деякий 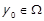 . Якщо цей елемент найбільший, то лема доведена. Інакше оскільки
. Якщо цей елемент найбільший, то лема доведена. Інакше оскільки 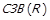 , то
, то  . Для
. Для 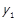 повторимо наведені міркування.
повторимо наведені міркування.
Нехай описаним вище чином вибрано  елементів, для яких
елементів, для яких 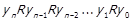 . Маємо
. Маємо  ,
,  . Через те, що
. Через те, що  скінченна, на деякому кроці t
скінченна, на деякому кроці t  . Покажемо, що
. Покажемо, що  буде єдиним найбільшим елементом. Нехай
буде єдиним найбільшим елементом. Нехай 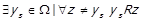 . Тоді
. Тоді 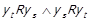 , що протирічить
, що протирічить  . Таким чином був знайдений єдиний на
. Таким чином був знайдений єдиний на  найбільший
найбільший  .
.
Доведено.
Теорема 1.6. Нехай задано 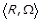 , і
, і 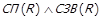 ,
, 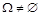 та
та  . Тоді на
. Тоді на  можна вибрати таке функціональне відображення
можна вибрати таке функціональне відображення  , що
, що 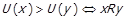 .
.
Доведення. Виберемо в  найбільший елемент
найбільший елемент  , за лемою 1.4 він єдиний. Звуження
, за лемою 1.4 він єдиний. Звуження 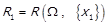 також буде відношенням строгого порядку. Позначимо
також буде відношенням строгого порядку. Позначимо 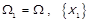 , та виберемо з неї найбільший елемент
, та виберемо з неї найбільший елемент  за
за 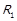 , та побудуємо
, та побудуємо  . Продовжуючи цей процес, отримаємо
. Продовжуючи цей процес, отримаємо
 .
.
Якщо тепер покласти 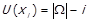 , U буде шуканим відображенням, оскільки за
, U буде шуканим відображенням, оскільки за 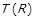
 .
.
Доведено.
Примітка 1.4 (до теореми 1.6). Відображення U для строгого порядку не є єдиним. Нехай 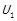 та
та 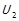 – два різних функціональних відображення, що задовольняють умові теореми 1.6 для одного і того ж самого відношення строгого порядку. Тоді можна показати, що існує
– два різних функціональних відображення, що задовольняють умові теореми 1.6 для одного і того ж самого відношення строгого порядку. Тоді можна показати, що існує 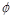 – монотонно зростаюча числова скалярна функція така, що
– монотонно зростаюча числова скалярна функція така, що 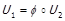 , де
, де 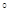 позначає композицію функцій.
позначає композицію функцій.
Примітка 1.5 (до теореми 1.6). Теорема залишається справедливою і у випадку, коли  – нескінченна злічена множина. Але результат вже не має місця, коли
– нескінченна злічена множина. Але результат вже не має місця, коли  – континуум. Покажемо це за допомогою контр-прикладу.
– континуум. Покажемо це за допомогою контр-прикладу.
Нехай  . З теорії множин відомо, що декартовий квадрат нескінченної множини рівнопотужний самій цій множині, зокрема має місце
. З теорії множин відомо, що декартовий квадрат нескінченної множини рівнопотужний самій цій множині, зокрема має місце 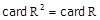 . Також очевидно, що
. Також очевидно, що 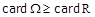 , і
, і  , звідки
, звідки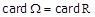 . Задамо наступне відношення лексикографічного порядку
. Задамо наступне відношення лексикографічного порядку 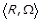 :
:
 .
.
Легко показати, що 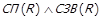 . Тепер нехай для R існує функціональне відображення U, що задовольняє умові теореми 1.6, тобто
. Тепер нехай для R існує функціональне відображення U, що задовольняє умові теореми 1.6, тобто
 .
.
Між двома різними дійсними числами 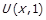 та
та  завжди можна обрати раціональне число
завжди можна обрати раціональне число 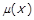 таке, що
таке, що 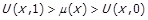 . Виберемо для деяких
. Виберемо для деяких  таких, що
таких, що
 ,
,
два 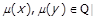 , і
, і
 .
.
Отримали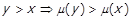 . Таким чином
. Таким чином 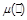 – бієкція між
– бієкція між 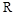 та
та  , що неможливо, оскільки ці множини не рівнопотужні.
, що неможливо, оскільки ці множини не рівнопотужні.
Примітка 1.6 (до теореми 1.6). Вимога слабкої зв’язності в умові теореми є суттєвою. Теорема не вірна для незв’язного строгого порядку.
Нестрогий порядок. Рефлексивне, транзитивне та антисиметричне відношення R називається відношенням нестрогого порядку. За допомогою предикатів це записується як  . Через рефлексивність це відношення може бути лише зв'язним та не може бути слабко зв'язним. «Нестрогість» цього відношення виражає наступне твердження.
. Через рефлексивність це відношення може бути лише зв'язним та не може бути слабко зв'язним. «Нестрогість» цього відношення виражає наступне твердження.
Лема 1.5. Нехай  та
та  . Тоді
. Тоді  на
на  для
для  .
.
Доведення.  можна отримати з
можна отримати з 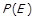 та інваріантності рефлексивності відносно операції об’єднання (теорема 1.2).
та інваріантності рефлексивності відносно операції об’єднання (теорема 1.2).
Далі, нехай  для деяких
для деяких 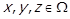 . Це означає, що можливі наступні випадки: 1)
. Це означає, що можливі наступні випадки: 1) 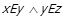 ; 2)
; 2) 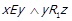 ; 3)
; 3)  ; 4)
; 4) 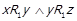 . Ці випадки взаємовиключні, оскільки
. Ці випадки взаємовиключні, оскільки 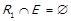 , бо
, бо 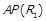 . У випадку 1
. У випадку 1 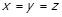 , і
, і  . У випадку 2
. У випадку 2 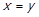 , і
, і  . Якщо справджується випадок 3, то
. Якщо справджується випадок 3, то 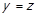 , та
, та  . Нарешті, у випадку 4 відповідно до
. Нарешті, у випадку 4 відповідно до 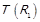
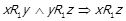 , і також
, і також  , що доводить
, що доводить 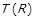 .
.
Тепер, 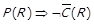 , це означає, що
, це означає, що 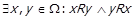 . Оскільки
. Оскільки  та
та 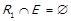 , знову маємо наступні взаємовиключні ситуації: 1)
, знову маємо наступні взаємовиключні ситуації: 1)  ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4) 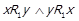 . Варіант 2 неможливий, оскільки
. Варіант 2 неможливий, оскільки 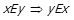 , але тоді
, але тоді 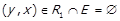 . Варіант 3 неможливий з аналогічних причин. Неможливий також і варіант 4 – через
. Варіант 3 неможливий з аналогічних причин. Неможливий також і варіант 4 – через  . Варіант 1 виконується тільки якщо
. Варіант 1 виконується тільки якщо 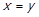 . Ми довели, що
. Ми довели, що 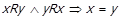 , тобто що
, тобто що  .
.
Доведено.
Справедливе в деякому розумінні зворотне твердження, яке дозволяє виділяти строгий порядок із нестрогого.
Лема 1.6. Нехай 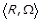 та
та  . Тоді
. Тоді  та
та 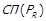 на
на  .
.
Доведення. Оскільки  , то
, то  . З
. З 
 ,
, 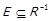 , і
, і 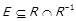 . Отже
. Отже 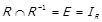 .
.
За означенням 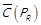 , а за теоремою 1.1
, а за теоремою 1.1  .
.  , тобто
, тобто
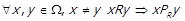 .
.
Оскільки 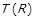 , то
, то 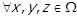 в тому числі і при
в тому числі і при 
 , а значить
, а значить 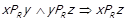 для таких елементів. Для
для таких елементів. Для 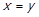
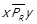 , а для
, а для 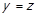
 , тобто такі випадки неможливі, і
, тобто такі випадки неможливі, і  доведено. Нарешті
доведено. Нарешті 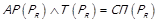 .
.
Доведено.
Нестрогий порядок має подібні до строгого порядку властивості. Наведемо їх нижче без доведення, яке аналогічне доведенням відповідних тверджень для строгого порядку.
Лема 1.7. Нехай задано 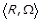 , і
, і  ,
, 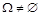 та
та  . Тоді існує єдиний найбільший по R елемент
. Тоді існує єдиний найбільший по R елемент  на
на  .
.
Без доведення.
Теорема 1.7. Нехай задано 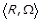 , і
, і  ,
,  та
та  – скінченна або злічена. Тоді на
– скінченна або злічена. Тоді на  можна вибрати таке функціональне відображення
можна вибрати таке функціональне відображення  , що
, що 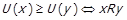 .
.
Без доведення.
Примітка 1.7 (до теореми 1.7). В якості U на скінченній  подібно до випадку строгого порядку можна взяти
подібно до випадку строгого порядку можна взяти 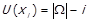 ,
, 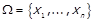 ,
, 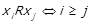 .
.
Квазіпорядок. Рефлексивне та транзитивне відношення називається відношенням квазіпорядку. Через предикати це записується як  Воно одночасно є узагальненням відношення еквівалентності та нестрогого порядку. Покажемо деякі властивості, які має квазіпорядок.
Воно одночасно є узагальненням відношення еквівалентності та нестрогого порядку. Покажемо деякі властивості, які має квазіпорядок.
Лема 1.8. Нехай 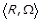 , та
, та 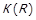 . Тоді
. Тоді  .
.
Доведення. За означенням 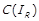 . Доведення випливає з теореми 1.2 про інваріантність відповідних властивостей відношення R відносно операцій із ним (розглядаються операції перетину та обернення), тобто
. Доведення випливає з теореми 1.2 про інваріантність відповідних властивостей відношення R відносно операцій із ним (розглядаються операції перетину та обернення), тобто  та
та 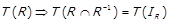 . Остаточно
. Остаточно
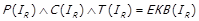 .
.
Доведено.
Для квазіпорядку R класи еквівалентності 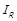 називаються областями рівня.
називаються областями рівня.
Теорема 1.8. Нехай 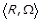 , та
, та 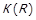 . Тоді
. Тоді  .
.
Доведення. Нехай  – розбиття (сімейство класів еквівалентності), яке відповідає еквівалентності
– розбиття (сімейство класів еквівалентності), яке відповідає еквівалентності 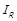 . Розглянемо деякий клас еквівалентності
. Розглянемо деякий клас еквівалентності  з цього розбиття.
з цього розбиття. 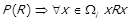 , тоді за означенням фактор-відношення
, тоді за означенням фактор-відношення  .
.
Тепер нехай для деяких класів еквівалентності 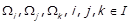 виконується
виконується  . Це означає, що для деяких представників
. Це означає, що для деяких представників  ,
,  виконано
виконано  , а для деяких
, а для деяких  та
та  виконано
виконано  . Оскільки
. Оскільки  , маємо
, маємо 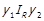 , а тим більше
, а тим більше  (оскільки
(оскільки  ). Отримали
). Отримали  , та за
, та за 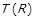
 . Для фактор-відношення це означає, що
. Для фактор-відношення це означає, що  . Ми показали, що
. Ми показали, що 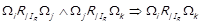 , тобто що
, тобто що 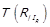 .
.
Те, що  означає, що для деяких
означає, що для деяких  . Припустимо, що одночасно виконується
. Припустимо, що одночасно виконується  , тобто що
, тобто що 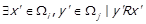 . Оскільки
. Оскільки  ,
, 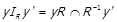 , а значить
, а значить 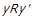 (оскільки ця пара належить перетину R із іншим відношенням). Відповідно до
(оскільки ця пара належить перетину R із іншим відношенням). Відповідно до 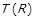
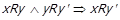 . Далі,
. Далі,  , маємо
, маємо 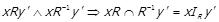 , тобто
, тобто 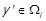 , і
, і  . Ми показали, що
. Ми показали, що  , що означає
, що означає 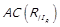 .
.
Остаточно 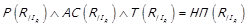 .
.
Доведено.
Має місце наступний наслідок цієї теореми.
Лема 1.9 (наслідок теореми 1.8). Нехай 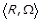 , та
, та 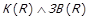 . Тоді
. Тоді  .
.
Доведення. В силу теореми 1.8 достатньо показати, що  . Розглянемо два довільні класи
. Розглянемо два довільні класи 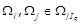 та довільні два їхні представники
та довільні два їхні представники  ,
, 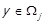 . Оскільки
. Оскільки  , то
, то 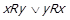 , що за означенням фактор-відношення означає
, що за означенням фактор-відношення означає  , тобто дійсно
, тобто дійсно  .
.
Доведено.
Слід не плутати поняття асиметричної частини 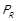 та фактор-відношення
та фактор-відношення 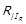 по симетричній частині. На рис. 1.3 представлені: граф квазипорядку R, графи
по симетричній частині. На рис. 1.3 представлені: граф квазипорядку R, графи  його симетричної та
його симетричної та 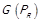 асиметричної частин, а також граф фактор-відношення
асиметричної частин, а також граф фактор-відношення 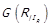 . Останній отримується стягуванням на
. Останній отримується стягуванням на 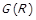 окремих компонент зв’язності
окремих компонент зв’язності  в єдину вершину, що відповідатиме деякому класу еквівалентності
в єдину вершину, що відповідатиме деякому класу еквівалентності 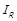 , який містить усі вершини цієї компоненти зв’язності.
, який містить усі вершини цієї компоненти зв’язності.

Рис. 1.3 – Графи відношень, пов’язаних із квазіпорядком 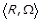 . На діаграмі б пунктирні дуги відносяться до симетричної частини
. На діаграмі б пунктирні дуги відносяться до симетричної частини 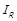 , суцільні – до асиметричної
, суцільні – до асиметричної 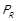
Знову розглянемо питання про існування спеціального виду функціонального відображення  на числову пряму для відношення R. Тепер візьмемо в якості R зв’язний квазіпорядок.
на числову пряму для відношення R. Тепер візьмемо в якості R зв’язний квазіпорядок.
Теорема 1.9. Нехай 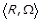 ,
, 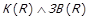 ,
, 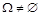 та
та  . Тоді на
. Тоді на  існує таке функціональне відображення
існує таке функціональне відображення  , що
, що 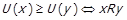 .
.
Доведення. Оскільки  (теорема 1.8), за теоремою 1.7 існує таке функціональне відображення
(теорема 1.8), за теоремою 1.7 існує таке функціональне відображення 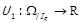 , що
, що  . Покладемо
. Покладемо 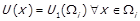 . По представникам різних класів еквівалентності умова теореми для U виконується, оскільки вона виконується для
. По представникам різних класів еквівалентності умова теореми для U виконується, оскільки вона виконується для 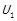 . Розглянемо деякі
. Розглянемо деякі 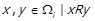 . Для них
. Для них 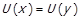 , тобто і в цьому випадку умови теореми виконані, і ми отримали шукане відображення.
, тобто і в цьому випадку умови теореми виконані, і ми отримали шукане відображення.
Доведено.
Примітка 1.8 (до теореми 1.9). Теорема справедлива також і для нескінченної зліченої  .
.
Примітка 1.9 (до теореми 1.9). Як і зазвичай, вимога  є суттєвою, і без неї теорема не має місця.
є суттєвою, і без неї теорема не має місця.
Слабке упорядкування. Асиметричне та від’ємно транзитивне відношення 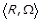 називається слабким упорядкуванням (впорядкуванням), або
називається слабким упорядкуванням (впорядкуванням), або 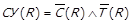 . Із взаємозв’язку властивостей бінарних відношень видно, що це частковий випадок строгого порядку, тобто
. Із взаємозв’язку властивостей бінарних відношень видно, що це частковий випадок строгого порядку, тобто  .
.
Поставимо у відповідність слабкому впорядкуванню R відношення непорівнянності 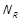 , що визначається як
, що визначається як 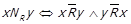 , або, що те ж саме,
, або, що те ж саме,  .
.
Введемо додаткове поняття. Нехай задані бінарні відношення  та
та  . Кажуть, що виконується узагальнена транзитивність
. Кажуть, що виконується узагальнена транзитивність 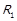 відносно
відносно  , або що
, або що 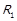 є транзитивним відносно відношення
є транзитивним відносно відношення  , якщо має місце
, якщо має місце
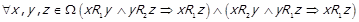 .
.
Це позначається як 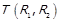 . Зрозуміло, що в загальному випадку
. Зрозуміло, що в загальному випадку  .
.
Для відношення непорівнянності 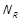 , де
, де 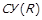 , справедливе наступне твердження.
, справедливе наступне твердження.
Лема 1.10. Нехай 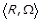 та
та 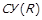 . Тоді
. Тоді  .
.
Доведення. Нехай 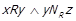 . Оскільки
. Оскільки 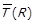 за лемою 1.3
за лемою 1.3  . Оскільки
. Оскільки 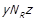 , то
, то 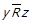 , тобто може виконуватись лише
, тобто може виконуватись лише  . Отже ми показали, що
. Отже ми показали, що 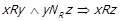 .
.
Тепер нехай 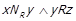 . Знову відповідно до
. Знову відповідно до 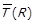
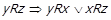 . Оскільки
. Оскільки  , то
, то 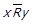 , тобто може виконуватись лише
, тобто може виконуватись лише  . Ми довели, що
. Ми довели, що  , отже остаточно
, отже остаточно  .
.
Доведено.
Доведемо важливу теорему щодо зв’язного впорядкування, з якої його природа як частковий випадок строгого порядку стає більш зрозумілою.
Теорема 1.10. Нехай задано 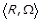 та
та 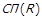 . Тоді
. Тоді  .
.
Доведення. ⇒ З означення 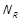 одразу випливає
одразу випливає  . Оскільки
. Оскільки  , то
, то  , а значить
, а значить 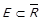 , отже
, отже  , а також
, а також 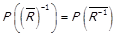 (лема 1.1). За теоремою 1.2 має місце
(лема 1.1). За теоремою 1.2 має місце 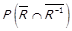 , тобто
, тобто 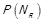 .
.
Припустимо, що для деяких 
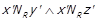 , але всупереч
, але всупереч 
 . Тоді
. Тоді 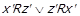 за означенням відношення непорівнянності. Оскільки
за означенням відношення непорівнянності. Оскільки 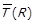 , за лемою 1.3
, за лемою 1.3  . Підставляючи
. Підставляючи  отримаємо
отримаємо 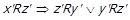 , а роблячи підстановку
, а роблячи підстановку 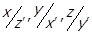 отримаємо
отримаємо  . Іншими словами, можливі наступні випадки:
. Іншими словами, можливі наступні випадки:  . Кожен з них протирічить
. Кожен з них протирічить  за означенням
за означенням 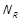 , і необхідність доведено.
, і необхідність доведено.
⇐ За теоремою 1.1 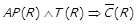 . Доведемо, що
. Доведемо, що 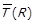 . Нехай навпаки для деяких
. Нехай навпаки для деяких 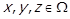
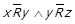 , але
, але  . З означення
. З означення 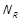
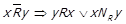 ,
,  . Можливі наступні випадки: 1)
. Можливі наступні випадки: 1)  ; 2)
; 2)  ; 3)
; 3) 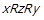 ; 4)
; 4) 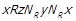 . Розглянемо кожний з цих випадків.
. Розглянемо кожний з цих випадків.
У випадку 1 через 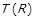
 , що протирічить
, що протирічить 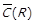 . У випадку 2 з
. У випадку 2 з 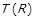 маємо
маємо  , що протирічить нашому припущенню
, що протирічить нашому припущенню 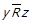 . У випадку 3 за
. У випадку 3 за 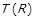 має виконуватись
має виконуватись 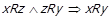 , що знову протирічить припущенню
, що знову протирічить припущенню 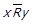 .
.
Розглянемо випадок 4. Оскільки за лемою 1.10  , то
, то  , що протирічить
, що протирічить  . Отже вихідне припущення невірне, тобто можливо лише
. Отже вихідне припущення невірне, тобто можливо лише 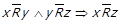 , звідки отримаємо
, звідки отримаємо 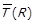 .
.
Остаточно 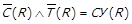 , і таким чином достатність доведена.
, і таким чином достатність доведена.
Доведено.
Оскільки для слабкого впорядкування R  , ми можемо виконати факторизацію R за відношенням непорівнянності. Результати викладемо у вигляді наступної теореми.
, ми можемо виконати факторизацію R за відношенням непорівнянності. Результати викладемо у вигляді наступної теореми.
Теорема 1.11. Нехай 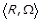 , та
, та 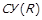 . Тоді
. Тоді 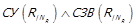 на
на 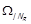 .
.
Доведення.
Доведено.
Як і для усіх інших класів бінарних відношень розглянемо питання про існування спеціального виду функціонального відображення  на числову пряму, але тепер R буде слабко зв’язним слабким упорядкуванням.
на числову пряму, але тепер R буде слабко зв’язним слабким упорядкуванням.
Теорема 1.12. Нехай 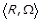 ,
, 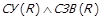 ,
, 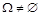 та
та  – скінченна або злічена. Тоді на
– скінченна або злічена. Тоді на  існує таке функціональне відображення
існує таке функціональне відображення  , що
, що 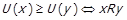 .
.
Доведення.
Доведено.
На цьому завершується огляд основних класів бінарних відношень. Зведемо в табл. 1.2 відомості про класи відповідно до властивостей, які повинні виконуватись для відношення, якщо воно належить до того чи іншого класу. Стовпцям таблиці відповідають окремі властивості відношень, а рядкам – класи. Відношень. Символом × у комірці таблиці відмічається та властивість, що присутня у означенні відповідного класу. Символом ⨂ натомість відмічається та властивість, що випливає з властивостей, помічених символом × для відповідного класу відношення.
| Таблиця 1.2. –Відомості про класи бінарних відношень відповідно до властивостей, виконання яких вимагається | ||||||||
| Клас | 
| 
| 
| 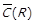
| 
| 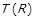
| 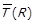
| 
|
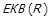
| × | × | × | |||||
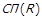
| × | ⨂ | × | ⨂ | ||||

| × | × | × | |||||
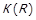
| × | × | ||||||
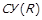
| ⨂ | × | ⨂ | × | ⨂ |
Також на рис. 1.4 показаний взаємозв’язок розглянутих класів відношень. Відношення квазіпорядку узагальнює відношення еквівалентності, нестрогого та строгого порядків (при розгляді симетричної 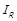 та асиметричної
та асиметричної 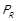 частин цього відношення). Натомість слабке впорядкування є частковим випадком строгого порядку, у якого відношення непорівнянності
частин цього відношення). Натомість слабке впорядкування є частковим випадком строгого порядку, у якого відношення непорівнянності 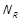 є еквівалентністю.
є еквівалентністю.

Рис. 1.4 – Взаємозв’язок класів бінарних відношень
|
|
|
|
|
Дата добавления: 2013-12-14; Просмотров: 2250; Нарушение авторских прав?; Мы поможем в написании вашей работы!