Малюнок 2. Круг Л.Ейлера

ПЛАН.

ББК

ББК

УДК

Додатки до плану цивільного захисту підприємств, установ, організацій щодо запобігання та реагування на НС техногенного та природного характеру

С

Розповсюдження та тиражування без офіційного дозволу заборонено

Р е ц е н з е н т и

1.

2.

Сілков В.В. Математика. Курс лекцій. Частина І.: Методичний посібник для студентів спеціальності 8.010102 «Початкове навчання», 8.010101 «Дошкільне виховання». – Рівне: РДГУ. 2006. - 86 с.

ISBN

Рекомендовано до друку Вченою радою Рівненського державного гуманітарного університету (протокол №?? від?? ________ 2006 р.)

ISBN

УДК

© В.В.Сілков, 2006.

© назва видавництва, 2006.

МОДУЛЬ 1: «Множини. Відповідності. Відношення.».

Змістовний модуль1.1. «Множини та операції над ними».

1. Поняття множини та її елементу, їхні позначення. Загальноприйняті позначення основних числових множин. Способи задання множин.

2. Порожня, скінченна, нескінченна та універсальна множини. Підмножина. Власні та невласні підмножини даної множини. Рівні та нерівні множини.

3. Відношення між множинами (включення, рівності, перерізу) та їх позначення за допомогою кругів Л.Ейлера та діаграм Ейлера-Венна. Потужність множини. Рівнопотужні (еквівалентні) множини. Скінченні, нескінченні та зчисленні множини. Множини потужності континууму.

4. Операція об’єднання (додавання) множин та основні властивості (закони) цієї операції.

5. Операція перетину множин та основні властивості (закони) цієї операції.

6. Операції різниці (віднімання) множин та основні властивості (закони) цієї операції.

7. Операція доповнення до даної та універсальної множини та основні властивості (закони) цих операцій.

8. Поняття розбиття множини на класи (підмножини), що попарно не перетинаються. Розбиття множини на класи за допомогою однієї, двох і трьох властивостей. Класифікації.

9. Поняття кортежу та впорядкованої пари. Поняття кортежу довжини n. Рівні пари та кортежі. Декартів (прямий) добуток множин, його задання та зображення. Властивості декартового добутку множин. Число елементів декартового добутку та об’єднання множин. Декартів добуток n множин.

ЛІТЕРАТУРА

[1] – Курс математики. – К.: Вища школа. 1995. - 392 с. (с. 3-40).

[2] – Кухар В.М., Білий Б.Н. Теоретичні основи початкового курсу математики. – К.: Вища школа, 1980. – 360 с. (с. 11-88).

[3] – Кухар В.М. та ін. Математика. Множини. Логіка. Цілі числа: Практикум. /За заг. ред. В.М.Кухар. – К.: Вища школа, 1989. – 333 с. (с. 5-56).

1. Поняття множини та її елементу, їхні позначення. Загальноприйняті позначення основних числових множин. Способи задання множин.

1. Якщо у повсякденному житті термін „множина” пов’язується, як правило, з великою кількістю предметів, то в математиці цим поняттям позначають різні множини незалежно від кількості елементів в них. Які ж множини розглядають в математиці? – ті, які містять один, два, три, тощо елементів, або навіть жодного елемента. У практичній діяльності термін «множина» має ряд синонімів: сукупність, колекція, клас, група, ансамбль. Хоча і в математиці існують синоніми для поняття «множина» (множина значень змінної – область визначення; множина двох рівнянь – система рівнянь тощо), але для математики важливо, щоб всі поняття трактувалися всіма однозначно. Саме тому виникає запитання «А що ж таке множина з точки зору математики?». Це поняття є одним із основних понять математики, але його означення не існує. Таким чином, поняття «множина» є, з одного боку, одним з основних понять математики, а з другого – неозначуваним, первісним. Сутність змісту цього поняття розкривається шляхом опису з допомогою конкретних прикладів. Отже, «множина» - це сукупність об’єктів певної природи, які можуть мати або не мати якусь спільну властивість. Поняття множини є основним поняттям спеціальної галузі математики - теорії множин. Теорія множин, як галузь математики, виникла в середині ХІХ століття. Її засновником вважають німецького математика Г.Кантора (1845-1918 рр.).

Множини прийнято позначати великими буквами латинського алфавіту: А, В, С,… Об’єкти, з яких складається множина, називають елементами множини. Їх прийнято позначати малими буквами латинського алфавіту: а, в, с, …, х, у або цими ж буквами з індексами. Якщо елемент а належить деякій множині М, то це позначають так: аÎМ, а якщо елемент в не належить множині А, то це позначають так: вÏА. Якщо деякі елементи належать множині А, то їх записують у фігурних дужках так: А={а, в, с, d}; В={в₁, в₂, в₃, в₄, в₅}.

Поняття множини широко використовують при вивченні різноманітних галузей математики. Деякі множини в математиці мають усталені, загальноприйняті позначення. Як відомо, множини можуть складатися із елементів будь-якої природи, зокрема із чисел. Такі множини прийнято називати числовими. Для деяких числових множин введені спеціальні позначення: множину натуральних чисел прийнято позначати буквою N={1, 2, 3, …, n, …}; множину цілих чисел позначають так: Z={0, ±1, ±2, ±3, … ±n, …}; множину раціональних чисел, яка складається із цілих чисел та додатних і від’ємних дробів прийнято позначати буквою Q; множину дійсних чисел, яка складається із множини раціональних та ірраціональних чисел позначають буквою R.

Задати множину означає: схарактеризувати її елементи так, щоб відносно кожного елемента можна було відразу встановити, належить він цій множині чи ні. Коли ж множина вважається заданою? – коли відносно будь-якого її елементу ми можемо твердити чи належить він множині чи ні. Як можна задати множину? – назвавши всі її елементи, тобто переліком. Задати множину переліком означає назвати чи записати всі її елементи, наприклад: М={1,2,3,4,5}. Що для цього слід зробити? – у фігурних дужках написати всі елементи множини, наприклад: А={а, в, с, d}, С={1, 2, 3, 4, 5, 6, 7, 8, 9, 0}. Чи завжди зручний розглянутий спосіб задання множин? Коли він зручний, а коли не зручний? – коли множина має малу кількість елементів; коли множина має велику кількість елементів.

Множини також можна задавати за допомогою характеристичної властивості, наприклад: А={х/хÎR і х>0}. Задати множину описом або за допомогою характеристичної властивості означає вказати характеристичну властивість всіх елементів множини, наприклад: множину натуральних чисел, які менші числа 6, описом задають так: М={х¤хÎNÙх<6}. Яким способом завжди можна задати множину? – за допомогою характеристичної властивості. Скінченні множини легко задавати і переліком, і описом. Але частіше користуються способом переліку. Нескінченні множини здебільшого задають описом. Але в окремих випадках задають і переліком, наприклад: Р={х/хÎNÙх:2}, М={2, 4, 6, 8,..., 2n,…}. Таким чином, існують два способи задання множин: описом або за допомогою характеристичної властивості та переліком.

2. Порожня, скінченна, нескінченна та універсальна множини. Підмножина. Власні та невласні підмножини даної множини. Рівні та нерівні множини.

2. У математиці розглядають множини, які не містять жодного елемента. Для їхнього позначення використовують спеціальний символ Æ, а називають їх порожніми множинами. Прикладом порожніх множин можуть бути такі: множина людей на Марсі; множина дійсних коренів рівняння х²+3=0. Нехай кількість елементів деякої множини А виражається натуральним числом. Для позначення цієї кількості використовують символ n(А), який читають так: число елементів множини А, або чисельність множини А, або потужність множини А. За кількістю елементів всі множини можна поділити на три групи: 1) порожні множини; 2) скінченні множини – це такі множини, кількість елементів яких можна позначити натуральним числом n(А). Прикладом скінченних множин можуть бути такі: множина цифр десяткової системи числення; множина студентів групи; 3) нескінченні множини – це такі множини, кількість елементів яких не можна виразити натуральним числом. Прикладами нескінченних множин є наступні: множина натуральних чисел; множина дійсних чисел.

Розглянемо кілька множин, які складаються із об’єктів однакової природи, наприклад: множина студентів першого курсу; множина студентів педагогічного факультету РДГУ; множина студентів РДГУ; множина студентів України; множина студентів світу. Як видно із наведеного прикладу, кожна наступна множина включає в себе попередню. Таку множину в математиці називають універсальною й позначають буквою U або інколи – І. Крім того, можна вважати, що існує множина, яка містить в собі всі множини, які тільки існують. По відношенню до однієї і тієї ж множини можна вибрати декілька універсальних множин. Так, для множини студентів другого курсу педагогічного факультету універсальною множиною можуть бути множина всіх студентів факультету, або множина студентів другого курсу РДГУ, або множина студентів м. Рівне. Для наочного зображення універсальної множини використовують прямокутник (див. малюнок 1).

и

Малюнок 1. Зображення універсальної множини.

Розглянемо дві множини А і В, таких, що кожен елемент множини В є елементом множини А, але в множині А є елементи, яких немає в множині В. У цьому випадку говорять, що множина В є підмножиною множини А. Це позначають так: BÌA або А É В, а читають: множина В є підмножиною множини А або В включається в А, або А включає В.

Означення: якщо кожен елемент множини В є елементом множини А, але в множині А є хоча б один елемент, яких немає в множині В, то множину В називають власною підмножиною множини А.

Символічно це записують так: BÌA або AÉB. Цей запис означає, що множина В включається в А і, що ці множини перебувають у відношенні включення. Підмножини бувають власні і невласні. Кожна скінченна не порожня множина А має дві невласні підмножини: 1) порожню (Æ); 2) саму себе (А).

Розглянемо деяку скінченну множину. Домовимося позначати множину всіх підмножин множини А символом Р(А), а число елементів множини Р(А) через n(Р(А)). Нехай А={2, 5, 7} і запишемо всі підмножини цієї множини. Це будуть: В₁={2}, В₂={5}, В₃={7}, В₄={2,5}, В₅={2,7}, В₆={5,7}, В₇=Æ, В₈=A={2,5,7}. Підмножини В₁, В₂, В₃, В₄, В₅ і В₆– власні, а В₇ і В₈ – невласні. Таким чином, Р(А)={Æ, А, {2}, {5}, {7}, {2,5}, {2,7}, {5,7}}. Отже, множина А, яка містила три елемента, має вісім підмножин. В математиці доведено, що число підмножин будь-якої скінченої множини визначається за формулою: n(p(A))=2^k, де n(p(A)) – число підмножин множини А, k – число елементів множини А, тобто n(A). Оскільки для множини А k=3, то n(p(A))=2³=8.

У теорії множин розглядаються множини, які складаються з одних і тих самих елементів. Про такі множини говорять, що вони рівні.

Означення 1: дві множини А та В називаються рівними, якщо кожна із них є підмножиною іншої, тобто: якщо АÌВ і ВÌА, то А=В.

Означення 2: якщо множини складаються з одних і тих самих елементів, то вони називаються рівними.

Означення 3: якщо кожен елемент множини А є елементом множини В і, навпаки, кожен елемент множини В є елементом множини А, то такі множини називаються рівними.

Як довести, що множина А дорівнює множині В? – показати, що кожен елемент множини А є елементом множини В, і, навпаки, кожен елемент множини В є елементом множини А, або показати, що кожна множина є підмножиною іншої, або показати, що множини складаються з одних і тих самих елементів.

3. Відношення між множинами (включення, рівності, перерізу) та їх позначення за допомогою кругів Л.Ейлера та діаграм Ейлера-Венна. Потужність множини. Рівнопотужні (еквівалентні) множини. Скінченні, нескінченні та зчисленні множини. Множини потужності континууму.

3. Ми розглянули означення рівності множин. За його допомогою між множинами можна задати відношення рівності. Які ж ще відношення можуть існувати між множинами? Виявляється, що це можуть бути відношення включення, перетину та рівності або тотожності. Для наочного зображення множин та відношень між ними використовуються спеціальні графічні зображення, на яких множини позначаються кругами або овалами. Такі круги прийнято називати кругами Л.Ейлера (див. малюнок 2). Якщо універсальну множину зображати прямокутником, а інші множини – кругами, то таке зображення має назву діаграм Ейлера-Венна (див. малюнок 3). На ньому зображено множину BÌAÌU. Відношення включення зображено на малюнку 4, а відношення перетину – на малюнку 5.

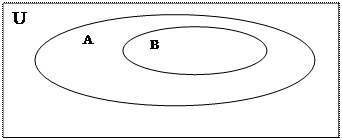
Малюнок 3. Діаграма Ейлера-Венна.

Малюнок 4: Відношення включення.

Малюнок 5: Відношення перетину.

Виконаємо мислено таку побудову: розіб’ємо всі скінченні множини на класи, у кожному з яких містяться лише рівночисельні множини і тільки вони. Термін клас тут вживається як синонім терміна «множина». Спільною властивістю всіх скінченних множин певного класу є кількість елементів або чисельність множини кожного класу, тобто натуральне число, яке є потужністю кожної множини певного класу. Хоча природа елементів кожної множини певного класу може бути різноманітною, але всі множини цього класу об’єднує одна спільна властивість, яку для скінченних множин називають рівночисельністю. Виникає запитання: чи можна аналогічно поставитися до нескінченних множин? Іншими словами, чи існують серед нескінченних множин нерівнопотужні множини. Деякий час вважали, що всі нескінченні множини рівнопотужні між собою. У 70-80-х роках ХІХ століття видатний німецький математики Г.Кантор встановив, що серед нескінченних множин є безліч нерівнопотужних між собою множин і що всі нескінченні множини також можна розбити на класи рівнопотужних множин. У результаті дістали узагальнення поняття натурального числа на випадок нескінченних множин у вигляді поняття кардинального числа.

Означення: потужністю або кардинальним числом певної множини М називають той клас Кα рівнопотужних множин, в якому ця множина знаходиться.

Усім множинам одного класу приписується одна й та сама потужність. Позначивши потужність множини М через n(М), дістанемо n(А)=n(В)↔А~В. Якщо в класі К_α містяться скінченні рівнопотужні множини, то потужністю кожної з них є натуральне число, що вказує на кількість елементів цієї множини. Якщо ж клас К_α містить нескінченні рівнопотужні множини, то потужністю кожної з них є кардинальне число n(М).

Таким чином, серед нескінченних множин є безліч нерівнопотужних між собою множин. Для них можна ввести шкалу потужностей аналогічно тому, як це зроблено для скінченних множин. Найменша нескінченна потужність – це той клас, в якому міститься множина натуральних чисел, тобто потужність множини натуральних чисел. Крім того, використовуючи поняття потужності можна більш чітко розглянути питання про скінченні та нескінченні множини. Враховуючи сказане, приймемо наступні означення.

Означення: множина називається нескінченною, якщо із неї можна виділити деяку підмножину, рівнопотужну даній множині.

Таким чином, множина є скінченною, якщо із неї не можна виділити підмножину еквівалентну даній.

Означення: множина називається зчисленною, якщо вона рівнопотужна множині натуральних чисел.

Означення: потужність множини дійсних чисел називають континуумом.

Прикладом зчисленних множин є множина раціональних чисел, множина парних чисел тощо. Для того, щоб перевірити зчисленною чи незчисленною є та чи інша множина, слід спробувати встановити взаємно однозначну відповідність між елементами цієї множини та множиною натуральних чисел.

4. Операція об’єднання (додавання) множин та основні властивості (закони) цієї операції.

4. Розглянемо дві множини: А={2,3,4} і В={2,4,6}. Утворимо нову множину С={2,3,4,6}. Із яких елементів складається множина С? – із елементів, які входять хоча б в одну із множин. Множину С, яка складається із елементів, що належать хоча б одній із множин А чи В, називають об’єднанням множин А і В. Її позначають С=АÈB.

Означення: Об’єднанням множин А та В називають третю множину АÈВ, що складається із елементів, які входять хоча б в одну із множин А чи В.

Символічно наведене означення можна записати так: АÈВ={х /хÎА або аÎВ}. На діаграмі Ейлера-Венна ця множина зображена на малюнку 6.

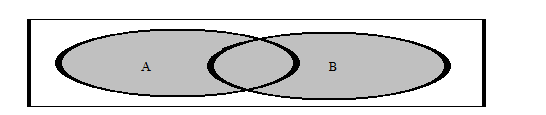
Малюнок 6: об’єднання множин АÈВ.

Операція об’єднання може поширюватись на три і більше множин. Вона підкоряється певним законам, серед яких є такі, справедливість яких випливає безпосередньо із означення об’єднання, та такі, які слід доводити. До законів (властивостей) об’єднання, справедливість яких легко обґрунтувати, виходячи із означення об’єднання множин, відносяться:

1. AÈÆ=A.

2. AÈU=U.

3. AÈA=A - закон ідемпотентності (незмінності).

До законів, які слід доводити одним із можливих способів (міркуваннями або за допомогою діаграм Ейлера-Венна) відноситься переставний або комутативний закон: AÈB=BÈA. Для його доведення використовуємо діаграми Ейлера-Венна. Намалюємо дві однакові діаграми, на лівій із яких зображатимемо ліву частину рівності, а на правій – праву. На лівій діаграмі заштрихуємо множину A горизонтальними штрихами, а множину B - вертикальними. Множина AÈB зображається тією частиною універсальної множини, де є або горизонтальні, або вертикальні штрихи. На правій діаграмі множину A заштрихуємо вертикальними штрихами, а множину В - горизонтальними. Множина BÈA зображається на правій діаграмі тією частиною універсальної множини, де є або вертикальні, або горизонтальні штрихи. Порівнюючи їх, бачимо, що множини AÈB і BÈA зображаються на них однаковими частинами універсальної множини, а тому можна стверджувати, що AÈB=BÈA. Закон доведено (див. малюнок 7).

АÈВ ВÈА

Малюнок 7: доведення переставного закону AÈB=BÈA.

Доведемо сполучний або асоціативний закон (AÈB)ÈС=AÈ(BÈС) за допомогою міркувань. Оскільки дві множини вважаються рівними, якщо кожен елемент першої множини є елементом другої і, навпаки, кожен елемент другої множини є елементом першої множини, то доведення складається з двох частин. У першій частині доведемо, що кожен елемент, що належить лівій частині асоціативного закону, є елементом і правої частини.

1. Нехай хÎ(AÈB)ÈС. Згідно означення об’єднання множин це означає, що: або 1) хÎ(AÈB), або 2) хÎС, або 3) хÎAÈB і хÎС. Якщо хÎAÈB, то або 1) хÎA, або 2) хÎB, або 3) хÎA і хÎB. Якщо хÎA, то, переходячи до правої частини закону, на основі означення об’єднання множин можна стверджувати, що хÎAÈ(BÈС). Якщо хÎB, то хÎBÈС, тобто хÎAÈ(BÈС). Якщо хÎA і хÎB, то хÎAÈ(BÈС). Якщо ж, нарешті, хÎС, то хÎ(BÈС), а тому хÎAÈ(BÈС). Таким чином ми показали, що будь-який елемент лівої частини рівності належить правій частині рівності. Оскільки елемент у лівій частині ми вибирали довільно, то наші міркування можна повторити для будь-якого елемента лівої частини. Отже, кожен елемент лівої частини рівності є елементом правої частини рівності. Перша частина теореми доведена.

2. Доведемо, що кожен елемент правої частини є елементом лівої. Нехай уÎAÈ(BÈС). Згідно означення об’єднання множин можливі такі випадки: або 1) уÎA, або 2) уÎBÈС, або 3) уÎA і уÎBÈС. Якщо уÎA, то уÎAÈB, а тому уÎ(AÈB)ÈС. Якщо уÎBÈС, то або 1) уÎB, або б) уÎС, або в) уÎB і уÎС. Якщо уÎB, то уÎAÈB тоді уÎ(AÈB)ÈС. Якщо уÎС, то уÎ(AÈB)ÈС. Якщо уÎB і уÎС, то уÎ(AÈB)ÈС. Аналогічно легко довести справедливість рівності у випадку, коли уÎA і уÎBÈС. Оскільки елемент у в правій частині ми вибрали довільно, то наші міркування можна повторити для кожного із елементів правої частини. Отже, кожен елемент правої частини є елементом лівої. Другу частину теореми доведено.

Таким чином, кожен елемент лівої частини є елементом правої частини і, навпаки. А тому, ліва і права частини рівності складаються з одних і тих самих елементів. А це означає, що (AÈB)ÈС=AÈ(BÈС). Закон доведено.

Приклад: утворити об’єднання множин А та В, якщо множина А={1,2,3,4,5}, а В={а,в,с}. AÈB={1,2,3,4,5,а,в,с}.

5. Операція перетину множин та основні властивості (закони) цієї операції.

5. Розглянемо дві множини А={1,2,3,4} і B={2,4,6,8} та утворимо третю множину С={2,4}. Із яких елементів складається множина С? – із елементів, які входять в кожну із множину, тобто із спільних елементів цих множин. Таку множину називають перетином множин А та В і позначають символом АÇВ=С.

Означення: перетином двох множин А і В називається така третя множина АÇВ, яка складається із спільних елементів А та В.

Символічно це означення можна записати так: AÇB={х/хÎA і хÎB}. З допомогою діаграм Ейлера-Венна перетин множин А і В зображено на малюнку 8. Означення перетину можна поширити на випадок трьох і будь-якої скінченної кількості множин. Операція перетину множин підкоряється таким законам:

1. AÇÆ=Æ.

2. AÇИ=A.

3. AÇA=A - закон ідемпотентності (незмінності).

4. AÇB=BÇA - переставний (комутативний).

5. АÇ(ВÇС)=(АÇВ)ÇС – сполучний (асоціативний).

6. АÇ(ВÈС)=(АÇВ)È(АÇС) – розподільний (дистрибутивний) закон перетину відносно об’єднання.

7. АÈ(ВÇС)=(АÈВ)Ç(АÈС) – розподільний (дистрибутивний) закон об’єднання відносно перетину.

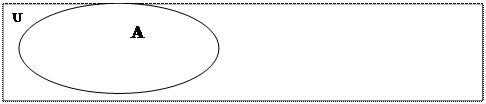Малюнок 8: перетин множин AÇB.

Справедливість законів 1-3 легко обґрунтувати, виходячи із означення операції перетину, а закони 4-7 слід довести, використовуючи міркування чи діаграми Ейлера-Венна. Доведемо асоціативний закон операції перетину (AÇB)ÇС=AÇ(BÇС), використовуючи діаграми Ейлера-Венна (див. малюнок 9). На лівій діаграмі спочатку заштрихуємо вертикальними лініями множину AÇB, а горизонтальними - множину С. Тоді множина (AÇB)ÇС зобразиться тією частиною універсальної множини, на якій штрихи накладуться. На правій діаграмі заштрихуємо спочатку вертикальними лініями множину BÇС, а множину А - горизонтальними. Тоді множина AÇ(BÇС) зобразиться тією частиною універсальної множини, на якій штрихи накладуться. Порівнюючи ліву та праву діаграми, бачимо, що множини (AÇB)ÇС і AÇ(BÇС) зображаються однієї й тією ж частиною універсальної множини. А це означає, що рівність (AÇB)ÇС=AÇ(BÇС) справедлива. Отже, закон доведено.

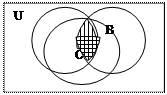Малюнок 9: доведення асоціативного закону операції перетину(AÇB)ÇС=AÇ(BÇС).

Операції об’єднання та перетину множин пов’язані між собою дистрибутивними або розподільними законами. Доведемо один із цих законів, а саме АÈ(ВÇС)=(АÈВ)Ç(АÈС), використовуючи міркування. Оскільки дві множини вважаються рівними тоді, коли кожен елемент першої є елементом другої, і навпаки, кожен елемент другої є елементом першої множини, то доведення складатиметься з двох частин. У першій частині доведемо, що кожен елемент лівої частини рівності належить правій, а в другій – що кожен елемент правої частини є елементом лівої. Виберемо у лівій частині рівності довільний елемент хєАÈ(ВÇС). Якщо хÎАÈ(ВÇС), то згідно означення операції об’єднання множин можливі два випадки: а) хєА і х Ï ВÇС; б) х Ï А і хєВÇС, тоді хєВ і хєС; в) хєА і хєВÇС, тоді хєА, хєВ і хєС.

а) якщо хєА і х Ï ВÇС, то х Ï В або х Ï С. Тоді, згідно означення операції об’єднання хє(АÈВ) і хє(АÈС), а згідно означення операції перетину хє(АÈВ)Ç(АÈС), тобто правій частині рівності.

б) якщо х Ï А і хєВÇС, то хєВ і хєС, а тому хє(АÈВ) і хє(АÈС). Отже, хє(АÈВ)Ç(АÈС), тобто правій частині рівності.

в) якщо хєА і хєВÇС, то згідно означення операції перетину хєВ і хєС. Тоді, згідно означення операції об’єднання хє(АÈВ) і хє(АÈС), а згідно означення операції перетину хє(АÈВ)Ç(АÈС), тобто правій частині рівності.

Таким чином, вибравши у лівій частині рівності довільний елемент, який їй належить, ми показали, що будь-який елемент лівої частини рівності належить правій частині рівності. Оскільки в лівій частині елемент ми вибирали довільно, то наші міркування можна повторити для будь-якого елемента лівої частини. Отже, кожен елемент лівої частини рівності є елементом правої частини рівності. Це означає, що (АÈ(ВÇС))Ì((АÈВ)Ç(АÈС)). Перша частина теореми доведена.

Проведемо доведення другої частини: покажемо, що кожен елемент правої частини рівності є елементом лівої. Нехай ує(АÈВ)Ç(АÈС). Тоді згідно означення операції перетину множин маємо: ує(АÈВ) і ує(АÈС). Тут можливі два випадки: а) уєА і уÏВ; б) уÏА і уєВ, а тоді уєС.

а) якщо уєА і уÏВ, то згідно означення операції об’єднання ує(АÈ(ВÇС)), тобто лівій частині.

б) якщо уєВ і уєС, то згідно означення операції перетину ує(ВÇС), а згідно означення операції об’єднання ує(АÈ(ВÇС)), тобто лівій частині. Таким чином, в обох випадках, якщо елемент належить правій частині, то він належить і лівій.

Оскільки елемент у правій частині ми вибрали довільно, то наші міркування можна повторити для кожного із елементів правої частини. Отже, кожен елемент правої частини є елементом лівої. Це означає, що справедливе твердження ((АÈВ)Ç(АÈС))Ì(АÈ(ВÇС)). Другу частину доведено.

Таким чином, у першій частині ми довели, що (АÈ(ВÇС))Ì((АÈВ)Ç(АÈС)), тобто, що кожен елемент лівої частини є елементом правої, а в другій частині – ((АÈВ)Ç(АÈС))Ì(АÈ(ВÇС)), тобто, що кожен елемент правої частини є елементом лівої. Отже, згідно означення рівності множин, маємо АÈ(ВÇС)=(АÈВ)Ç(АÈС), тобто ліва і права частини рівності складаються з одних і тих самих елементів. А це означає, що справедливість закону доведено.

Готуючись до екзамену студент має право доводити відповідні закони будь-яким із наведених способів. Для оволодіння способами доведення пропонуємо студентам довести самостійно всі не доведені закони будь-яким із запропонованих двох способів.

6. Операції різниці (віднімання) множин та основні властивості (закони) цієї операції.

6. Розглянемо дві множини А={1,2,3,4} і B={2,4,6,8} та утворимо третю множину С={1,3}. Із яких елементів складається множина С? – із елементів, які входять у множину А, але не входять у множину В. Таку множину називають різницею множин А та В і позначають символом А\В=С.

Означення: різницею двох множин А і В називається така третя множина А\В, яка складається із тих і тільки тих елементів множини А, що не належать множині В.

Символічно це означення можна записати так: A\B={х/хÎA і хÏB}.

Операцію знаходження різниці двох множин називають відніманням. Якщо ВÌА, то А\В називається доповненням множини В до множини А. За допомогою кругів Ейлера різницю множин А і В зображено на малюнку 10. Різні випадки різниці множин за допомогою кругів Ейлера можна зобразити так (див. малюнки 11-14).

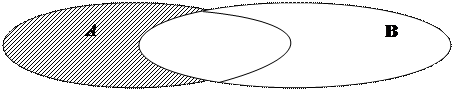Малюнок 10: різниця множин А\В.

Малюнок 11: різниця множин А\В. Малюнок 12: різниця множин А\В.

U

U

Малюнок 13: різниця множин В\А=Æ. Малюнок 14: різниця множин А\В=А.

За допомогою діаграм Ейлера-Венна легко довести, що операція різниці не підкоряється комутативному закону, тобто, що А\В¹В\А (див. малюнки 15-16).

Малюнок 15: А\В. Малюнок 16: В\А.

7. Операція доповнення до даної та універсальної множини та основні властивості (закони) цих операцій.

7. Із поняттям різниці множин тісно пов’язана операція доповнення даної множини до універсальної. Це важливо, оскільки певні сукупності ми розглядаємо у рамках відповідної універсальної множини U. У таких випадках операція знаходження доповнення множин набуває самостійного значення, хоч вона є окремим випадком операції віднімання множин.

Означення: Доповненням даної множини AÌU до універсальної множини U називається множина U\A, яка є різницею цих множин, тобто така множина, яка містить усі ті і тільки ті елементи множини U, що не належать множині А.

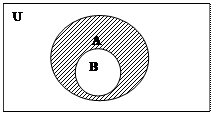
Доповнення даної множини до універсальної позначають Ā або інколи А'. Символічно прийняте означення можна записати так: Ā={х/хÎU і хÏA}. Графічне зображення множини Ā представлено на діаграмі Ейлера-Венна (див. малюнок 17).

Малюнок 17: доповнення множини А до універсальної множини U: Ā=U\А.

Безпосередньо із означення доповнення випливає справедливість таких законів:

1. Ū=Æ. 2. Æ'= U. 3. А"=А - закон подвійного доповнення.

Операції доповнення, перетину і об’єднання множин пов’язані між собою законами де Моргана:

1. (AÈB)'=A'ÇB' - доповнення до об¢єднання множин А і В дорівнює перетину доповнень цих множин.

2. (AÇB)'=A'ÈB' - доповнення до перетину множин А і В дорівнює об’єднанню доповнень цих множин.

Довести ці закони можна як міркуваннями, так і за допомогою діаграм Ейлера-Венна. Доведемо перший закон (AÈB)'=A'ÇB' за допомогою міркувань. Спочатку доведемо, що кожен елемент лівої частини є елементом правої. Якщо хÎ(AÈB)', то згідно означення доповнення це означає, що хÏAÈB, а відповідно до означення об’єднання хÏA і хÏB. Тоді згідно означення доповнення хÎА' і хÎB', а тому згідно означення операції перетину хÎА'ÇB', тобто правій частині. Оскільки елемент х у лівій частині ми вибирали довільно, то наші міркування можна повторити відносно будь-якого елемента лівої частини. Отже, кожен елемент лівої частини належить і правій частині рівності, а тому (AÈB)'ÌA'ÇB'. Першу частину доведено.

Доведемо, що кожен елемент правої частини є елементом лівої. Нехай уÎA'ÇB'. Згідно означення перетину множин це означає, що уÎA' і уÎB', а тоді відповідно до означення доповнення це означає, що уÏA і уÏB. Згідно до означення об’єднання уÏAÈB, а тому відповідно до означення доповнення уÎ(AÈB)', тобто лівій частині. Оскільки елемент у в правій частині ми вибирали довільно, то наші міркування можна повторити відносно будь-якого елемента правої частини. Отже, кожен елемент правої частини належить і лівій частині рівності, а тому (A'ÇB')Ì(AÈB)'. Другу частину доведено.

Таким чином, у першій частині ми довели, що (AÈB)'ÌA'ÇB', а у другій, що (A'ÇB')Ì(AÈB)'. Згідно означення рівності множин це означає, що (A'ÇB')=(AÈB)', тобто закон доведено повністю.

Доведемо другий закон (AÇB)'=A'ÈB' за допомогою діаграм Ейлера-Венна. Ліву частину рівності будемо зображати на лівій діаграмі, а праву частину – на правій. На лівій діаграмі множину AÇB заштрихуємо вертикальними лініями. Тоді доповнення цієї множини до універсальної, тобто множину (AÇB)', заштрихуємо на лівій діаграмі горизонтальними лініями. Отже, елементи, які належать лівій частині рівності, знаходяться у тій частині універсальної множини, на якій є горизонтальна штриховка. На правій діаграмі множину А' заштрихуємо вертикальними лініями, а множину В' – горизонтальними лініями. Тоді на правій діаграмі множина А'ÈB' буде зображатися тією частиною універсальної множини, де є хоча б одна штриховка, або вертикальними, або горизонтальними лініями.

Порівнюючи ліву і праву частини діаграми, бачимо, що на лівій діаграмі множина (AÇB)' зображається всією універсальною множиною без множини AÇB; на правій діаграмі множина A'ÈB' також зображається елементами універсальної множини без множини AÇB. Таким чином, ліва і права частини рівності, що виражає закон де Моргана, зображається однаковими частинами універсальної множини, а тому він справедливий, тобто правильна рівність (AÇB)'=A'ÈB' (див. малюнок 18).

Малюнок 18: доведення закону де Моргана (AÇB)'=A'ÈB'.

8. Поняття розбиття множини на класи (підмножини), що попарно не перетинаються. Розбиття множини на класи за допомогою однієї, двох і трьох властивостей. Класифікації.

8. Розглянемо множину студентів педфаку, позначивши її А. Розглянемо на цій множині властивість «бути однокурсником». За допомогою цієї властивості множина А розіб’ється на п’ять підмножин: А₁ – множина студентів І курсу; А₂ - множина студентів ІІ курсу; А₃ – множина студентів ІІІ курсу; А₄ – множина студентів ІУ курсу; А₅ – множина студентів У курсу. Що характерне для цих множин? - 1) вони не порожні; 2) вони попарно не перетинаються; 3) об’єднання цих підмножин дає нам множину А, тобто А₁ÈА₂ÈА₃ÈА₄ÈА₅=А. В таких випадках говорять, що ми маємо справу із розбиттям множини на підмножини (класи), що попарно не перетинаються.

Чи можна розбити множину А іншим способом? – так, якщо розглянути ще одну властивість, наприклад, „навчатися на державній формі фінансування”. Скільки підмножин ми при цьому отримаємо? – оскільки кожна із підмножин А₁, А₂, А₃, А₄ і А₅ розіб’ється в свою чергу ще на п’ять підмножин, то всього за допомогою двох властивостей одержимо десять підмножин: А₁₁ – множина студентів І курсу, які навчаються на державній формі фінансування; А₁₂ – множина студентів І курсу, які навчаються на платній формі фінансування; А₂₁ – множина студентів ІІ курсу, які навчаються на державній формі фінансування; А₂₂ – множина студентів ІІ курсу, які навчаються на платній формі фінансування; А₃₁ – множина студентів ІІІ курсу, які навчаються на державній формі фінансування; А₃₂ – множина студентів ІІІ курсу, які навчаються на платній формі фінансування; А₄₁ – множина студентів ІУ курсу, які навчаються на державній формі фінансування; А₄₂ – множина студентів ІУ курсу, які навчаються на платній формі фінансування; А₅₂ – множина студентів У курсу, які навчаються на державній формі фінансування; А₅₂ – множина студентів У курсу, які навчаються на платній формі фінансування. Що характерне для цих підмножин? - 1) вони також не порожні; 2) вони попарно не перетинаються; 3) вони в об’єднанні дають всю множину А. В таких випадках говорять, що ми маємо справу із розбиттям множини на підмножини (класи), що попарно не перетинаються.

Якщо крім названих двох властивостей розглянути ще одну властивість „проживати у сільській місцевості”, то кожна із отриманих раніше підмножин розіб’ється на дві, а тому ми отримаємо у множині А з допомогою трьох властивостей двадцять підмножин: А₁₁₁ – множина студентів І курсу, які навчаються на державній формі фінансування і проживають у сільській місцевості; А₁₁₂ – множина студентів І курсу, які навчаються на платній формі фінансування і не проживають у сільській місцевості; А₁₂₁ – множина студентів І курсу, які навчаються на платній формі фінансування і проживають у сільській місцевості; А₁₂₂ – множина студентів І курсу, які навчаються на платній формі фінансування і не проживають у сільській місцевості; А₂₁₁ – множина студентів ІІ курсу, які навчаються на державній формі фінансування і проживають у сільській місцевості; А₂₁₂ – множина студентів ІІ курсу, які навчаються на платній формі фінансування і не проживають у сільській місцевості; А₂₂₁ – множина студентів ІІ курсу, які навчаються на платній формі фінансування і проживають у сільській місцевості; А₂₂₂ – множина студентів ІІ курсу, які навчаються на платній формі фінансування і не проживають у сільській місцевості; А₃₁₁ – множина студентів ІІІ курсу, які навчаються на державній формі фінансування і проживають у сільській місцевості; А₃₁₂ – множина студентів ІІІ курсу, які навчаються на платній формі фінансування і не проживають у сільській місцевості; А₃₂₁ – множина студентів ІІІ курсу, які навчаються на платній формі фінансування і проживають у сільській місцевості; А₃₂₂ – множина студентів ІІІ курсу, які навчаються на платній формі фінансування і не проживають у сільській місцевості; А₄₁₁ – множина студентів ІУ курсу, які навчаються на державній формі фінансування і проживають у сільській місцевості; А₄₁₂ – множина студентів ІУ курсу, які навчаються на платній формі фінансування і не проживають у сільській місцевості; А₄₂₁ – множина студентів ІУ курсу, які навчаються на платній формі фінансування і проживають у сільській місцевості; А₄₂₂ – множина студентів ІУ курсу, які навчаються на платній формі фінансування і не проживають у сільській місцевості; А₅₁₁ – множина студентів У курсу, які навчаються на державній формі фінансування і проживають у сільській місцевості; А₅₁₂ – множина студентів У курсу, які навчаються на платній формі фінансування і не проживають у сільській місцевості; А₅₂₁ – множина студентів У курсу, які навчаються на платній формі фінансування і проживають у сільській місцевості; А₅₂₂ – множина студентів У курсу, які навчаються на платній формі фінансування і не проживають у сільській місцевості. Які ж властивості мають вказані підмножини? – такі ж самі, як і попередніх випадках. Чи може хтось сформувати означення розбиття множини на підмножини, що попарно не перетинаються?

Означення: Система S непорожніх підмножин даної множини М називається розбиттям множини М на підмножини (класи), що попарно не перетинаються, якщо кожний елемент мÎМ належить одній і тільки одній підмножині з Ѕ, тобто, якщо:

1) кожен елемент з множини Ѕ є підмножиною множини М;

2) кожен елемент з Ѕ є непорожньою множиною;

3) елементи з множини Ѕ попарно не перетинаються;

4) об’єднання всіх елементів з Ѕ утворює множину М, тобто, кожен елемент з множини М належить одній з підмножин розбиття Ѕ.

Поняття розбиття множин на підмножини, що попарно не перетинаються, широко використовуються при проведенні класифікацій. Прикладом класифікацій у математиці може бути поділ кутів на прямі і непрямі, натуральних чисел на парні і непарні тощо. У біології це поділ організмів на живі та неживі, у бібліотекознавстві – різноманітні каталоги. Разом з тим зазначимо, що для правильного проведення класифікації слід дотримуватися вказаних в означенні умов. Якщо хоча б одна із вказаних умов буде порушена, то класифікація стане неправильною.

9. Поняття кортежу та впорядкованої пари. Поняття кортежу довжини n. Рівні пари та кортежі.

9. Що можна сказати про порядок розміщення елементів у множині? – у загальному випадку він не має принципового значення. Але для певних множин він важливий. Перейдемо до розгляду упорядкованих множин. Число 39 можна записати за допомогою двох цифр 3 і 9. Ці цифри слід ставити в певному порядку: спочатку 3, а потім 9. Якщо їх переставити, то одержимо інше число, а саме 93. Говорять, що (3;9) – це впорядкована пара чисел. Впорядкова­ну пару чисел х і у будемо записувати таким, чином: (х;у). Число 55 записується за допомогою двох однакових цифр, тобто цифри утворюють впорядковану пару чисел (5;5). Таким чином, у впорядкованих парах елементи можуть повторюватися. Впорядковані пари можна складати не лише із чисел, а також і з елементів будь-яких множин.

Означення: Упорядкованою парою або кортежем довжини 2 називають таку множину з двох елементів а і в, у якій істотним є не тільки самі елементи, але й порядок їх розміщення у множині (а,в).

Елементи впорядкованої пари називаються компонентами або координатами. Впорядковану пару (а,в) ще називають кортежем довжини 2 і позначають <а,в>. Аналогічно можна визначити поняття впорядкованої трійки або кортежу довжини три, впорядкованої четвірки або кортежу довжини чотири тощо. Як би ви ввели поняття кортежу довжини к? – впорядкована множина, яка містить к елементів, тобто (а₁,а₂,а₃,...,а_к). Прикладом впорядкованих трійок можуть бути: (2,1,3), (2,2,3), (1,2,8) тощо.

Означення: Дві пари (а,в) і (с,d) називаються рівними, якщо відповідні компоненти їх рівні, тобто (а,в)=(с,d) тоді і тільки тоді, коли а=с і в=d.

Розглянемо дві множини Х={а,в,с} і У={3,9}. Утворимо із елементів цих множин пари таким чином, щоб перша компонента пари належала множині X. а друга - множині У. Всі пари ут­ворять множину: {(а,3), (а,9), (в,3), (в,9), (с,3), (с,9)}. Її називають декартовим (або прямим) добутком множин Х і У і позначають Х´У.

Означення: декартовим добутком множин Х і У називається множина Х´У впорядкованих пар (х;у) таких, що хєХ і уєУ.

Символічно це означення можна записати так: Х´У={(х;у)/хєХ і уєУ}. Якщо множини Х і У співпадають, тобто Х=У, то множина Х´Х складається із всіх пар (х;х) таких, що хєХ і називається декартовим квадратом. Вона позначається Х². Аналогічно можна означити декартів добуток трьох, чотирьох і будь-якого скінченного числа множин.

Означення: декартовим добутком множин А₁, А₂,..., А_n називається множина кортежів (а_1, а₂,_, а₃,...,а_n) довжини n таких, що а₁ÎА_1, а₂ÎА₂, а₃ÎА₃, …, а_nÎА_n, тобто А₁´А₂´А₃´..´А_n={(а_1, а₂,_, а₃,...,а_n)/а₁ÎА_1, а₂ÎА₂, а₃ÎА₃, …, а_nÎА_n }.

Як же можна задавати декартів добуток множин? – оскільки декартів добуток є множиною, то його можна задавати тими ж способами, що і множини, тобто: 1) переліком всіх пар, що входять до нього, наприклад Х´У={(а,3), (а,9), (в,3), (в,9), (с,3), (с,9)}; 2) описом або за допомогою характеристичної властивості, наприклад: Х´У={(х;у)/хÎХ і уÎУ}. Крім того, декартів добуток множин можна задавати ще й такими способами: 3) табличним, коли елементи, які належать декартовому добутку множин розміщують у вигляді таблиці, в якій у стовпчиках розміщені елементи множини X, а в рядках - елементи множини У, а елементи множини Х´У пишуть на перетині відповідних рядків і стовпців (див. малюнок 19); 4) аналітично, тобто за допомогою формули, наприклад: у=5х-7; 5) графічно, коли елементи декартового добутку множин зображаються точками декартової прямокутної системи координат; 6) за допомогою графа (див. малюнок 20).

Розглянемо властивості декартового добутку множин.

1. А´В¹В´А – ця нерівність говорить про те, що декартів добуток множин немає властивості комутативності.

2. (АÈВ)´С=(А´С)È(В´С).

3. А´(ВÈС)=(А´В)È(А´С).

4. (АÇВ)´С=(А´С)Ç(В´С).

5. А´(ВÇС)=(А´В)Ç(А´С).

6. (А\В)´С=(А´С)\(В´С).

7. А´(В\С)=(А´В)\(А´С).

у х	а	в	С
	(1,а)	(1,в)	(1,с)
	(3,а)	(3,в)	(3,с)
	(5,а)	(5,в)	(5,с)
	(7,а)	(7,в)	(7,с)

Таблиця № 1. Табличне задання декартового добутку множин.

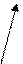
а в

с 1 2

3 4 5

6

Дата добавления: 2013-12-14