Малюнок № 2. Графік рівняння у=kx

Малюнок 1. Графік рівняння кола.

Виберемо систему координат і в ній пряму, яка проходить через початок координат. Виберемо на цій прямій точку 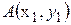, яка відмінна від точки 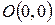. Нехай для простоти викладок точка А лежить в першій чверті (див. малюнок № 2).

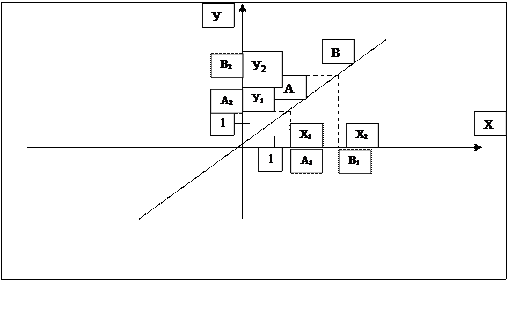
Відношення у₁:х₁ не залежить від вибору точки на прямій. Для доведення цього факту візьмемо на прямій ще одну точку . Розглянемо трикутники ОАА₁ та ОВВ₁. Оскільки ці трикутники подібні, то із подібності трикутників маємо АА₁:ОА₁=ВВ₁:ОВ₁. Але АА₁=у₁, ОА₁=х₁, ВВ₁=у₂ ОВ₁=х₂. Звідси у₁:х₁=у₂:х₂. Це співвідношення і показує, що відношення у:х не залежить від вибору точки на прямій. Отже, y:х=k. Аналогічні результати ми одержимо, коли візьмемо точки в інших координатних чвертях. Число k характеризує нахил прямої до додатного напрямку осі абсцис. Це відношення дорівнює тангенсу кута між віссю абсцис та прямою . Таким чином, для будь-якої точки, що лежить на прямій, крім точки О, виконується рівність 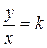. Помноживши обидві частини рівняння на х, маємо . Це співвідношення виконується і для точки 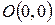, бо . Рівняння виду у=kх називають рівнянням прямої, яка проходить через початок координат. Крім цього, k=tgα, де α – кут нахилу прямої у=kх до додатного напрямку осі абсцис.

Доведемо обернене: будь-яка точка М₁(х₁;у₁), координати якої задовольняють рівняння у=kх, належить прямій, що задається рівнянням у=kх. Дійсно на прямій у=kx завжди є точка К з абсцисою х₁, тобто К(х₁;у). Тоді ордината у цієї точки дорівнює kx₁. Отже, К(х₁; kx₁). Це означає, що у=у, тобто К і 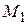співпадають. Таким чином, точка М₁ лежить на прямій. Ми довели, що при заданому значенні k рівнянню у=kх задовольняють координати точок, які розміщені на деякій прямій лінії, яка проходить через початок координат, і не задовольняють координати точок, які не лежать на цій прямій (малюнок № 2).

Число k називають кутовим коефіцієнтом прямої. З’ясуємо, який знак має коефіцієнт k в залежності від того, де розміщена пряма? – для цього визначимо знак частки у:х. Ця частка додатна для точок, які розміщенні в І і ІІІ координатних чвертях, і від’ємна – для точок, розміщених в ІІ і ІV чвертях. Таким чином, значення k буде додатнім для прямих, які проходять в І та ІІІ чверті, а від’ємне для прямих, розміщених в ІІ та ІV чверті.

Проведемо тепер пряму, яка буде паралельна прямій y=kx і відсікатиме на осі ординат відрізок довжини b. Виберемо на цій прямій довільну точку М(х;у) і опустимо із неї перпендикуляр ММ' на вісь абсцис. Позначимо через М₁ точку перетину цього перпендикуляра з прямою у=kх. Із малюнка № 2 видно, що ММ'=ММ₁+М₁М'. Але ордината М₁М' точки М₁ дорівнює kx, а ММ₁=b. Отже, у=ММ₁=ММ₁+М₁М'=kx+b. Таким чином, ми довели, що координати будь-якої точки прямої задовольняють рівнянню у=kx+b. Отже, пряма має рівняння у=kx+b. Число b називають початковою ординатою прямої, а рівняння виду у=kx+b – рівнянням прямої з кутовим коефіцієнтом.

Розглянемо дві прямі L₁ та L₂ які не проходять через початок координат. якщо прямі паралельні, то вони будуть паралельними одній і тій же прямій, яка проходить через початок координат. Що можна сказати про кутові коефіцієнти цих прямих? – вони будуть однакові. Навпаки, якщо кутові коефіцієнти цих прямих рівні, то прямі паралельні прямій, яка проходить через початок координат. Таким чином, для того, щоб дві прямі були паралельні (якщо жодна із них не паралельна осі координат), необхідно і достатньо, щоб їх кутові коефіцієнти були рівними. Сказане символічно можна записати так: k₁=k₂.

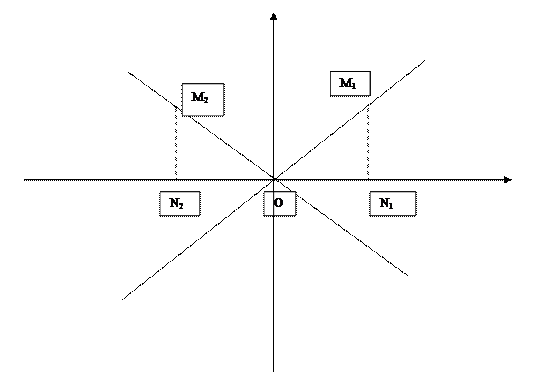
Виведемо умову перпендикулярності двох прямих. Проведемо через початок координат дві взаємно перпендикулярні прямі у=k₁x і y=k₂x. Одна із цих прямих утворює з додатнім напрямком осі абсцис гострий кут, а друга – тупий. Тоді знаки кутових коефіцієнтів цих прямих різні, один додатній, а другий – від’ємний. На першій прямій виберемо точку М₁(х₁;у₁), а на другій – точку М₂(х₂;у₂) (див. малюнок № 3).

Дата добавления: 2013-12-14