Мостикові схеми

Мостикова структура (рис. 2.4, а, б) являє собою паралельне з'єднання послідовних ланцюжків елементів з діагональними елементами, включеними між вузлами різних паралельних областей (елемент 3 на рис. 2.4, а, елементи 3 і 6 на рис. 2.4, б). Працездатність такої системи визначається не тільки кількістю елементів, що відмовили, але і їхнім положенням в структурній схемі. Наприклад, працездатність ТС, схема якої наведена на рис.2.4, а, буде втрачена при одночасній відмові елементів 1 і 2, або 4 і 5, або 2, 3 і 4 тощо.

В той же час відмова елементів 1 і 5, або 2 і 4, або 1, 3 і 4, або 2, 3 і 5 до відмови системи не призводить. Для розрахунку надійності мостикових систем можна скористатися методом прямого перебору, як це було зроблено для систем “m з n“, але при аналізі працездатності кожного стану системи необхідно враховувати не тільки число елементів, що відмовили, але і їхнє положення в схемі.

Метод прямого перебору ефективний тільки при малій кількості елементів n, про що говорилося на початку розділу, оскільки число станів системи становить 2ⁿ. Наприклад, для схеми на рис. 2.4,б їхня кількість складе вже 256. Деяке спрощення досягається, якщо в таблицю станів включати тільки сполучення, що відповідають працездатному (або тільки непрацездатному) стану системи в цілому.

Для аналізу надійності ТС, структурні схеми яких не зводяться до паралельного або послідовного типу, можна скористатися методом логічних схем із застосуванням алгебри логіки (булевої алгебри). Застосування цього методу зводиться до складання для ТС формули алгебри логіки, що визначає умову працездатності системи. При цьому для кожного елемента і системи в цілому розглядаються дві протилежних події - відмова і збереження працездатності. Для складання логічної схеми можна скористатися двома методами - мінімальних шляхів і мінімальних перетинів.

Розглянемо метод мінімальних шляхів для розрахунку ймовірності безвідмовної роботи на прикладі мостикової схеми (рис. 2.4,а).

Мінімальним шляхом називається послідовний набір працездатних елементів системи, що забезпечує її працездатність, а відмова кожного з них приводить до її відмови.

Мінімальних шляхів в системі може бути один або декілька. Очевидно, система з послідовним з'єднанням елементів (рис. 2.1) має тільки один мінімальний шлях, що включає всі елементи. В системі з паралельним з'єднанням (рис. 2.2) число мінімальних шляхів збігається із числом елементів і кожний шлях включає один з них.

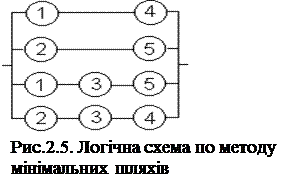
Для мостикової системи з п'яти елементів (рис. 2.4,а) мінімальних шляхів чотири: (елементи 1 і 4), (2 і 5), (1, 3 і 5), (2, 3 і 5). Логічна схема такої системи (рис. 2.5) складається таким чином, щоб всі елементи кожного мінімального шляху були з'єднані один з одним послідовно, а всі мінімальні шляхи паралельно.

Потім для логічної схеми складається функція алгебри логіки А за загальними правилами розрахунку ймовірності безвідмовної роботи, але замість символів ймовірностей безвідмовної роботи елементів 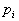і системи Р використовуються символи події (збереження працездатності елемента a_i і системи А).

Так, “відмова“ логічної схеми рис. 2.5 складається з одночасної відмови всіх чотирьох паралельних областей, а “безвідмовна робота” кожної області - в одночасній безвідмовній роботі її елементів. Послідовне з'єднання елементів логічної схеми відповідає логічному множенню (“І”), паралельне - логічному додаванню (“АБО”).

Отже, схема рис. 2.5 відповідає твердженню: система працездатна, якщо працездатні елементи 1 і 4, або 2 і 5, або 1,3 і 5, або 2,3 і 4. Функція алгебри логіки запишеться:

А=1-(1-а₁а₄)(1-а₂а₅)(1-а₁а₃а₅)(1-а₂а₃а₄) (2.7)

У виразі (2.7) змінні а розглядаються як булеві, тобто можуть прийматися тільки два значення: 0 або 1. Тоді при зведенні в будь-який ступінь k будь-яка змінна a зберігає своє значення:. На основі цієї властивості функція алгебри логіки (2.7) може бути перетворена до виду:

А=а₁а₄+а₂а₅+а₁а₃а₄+а₂а₃а₄­­-а₁а₂а₃а₄-а₁а₂а₃а₅-2а₁а₂а₄а₅-а₂а₃а₄а₅-

-а₂а₃а₄а₅+2а₁а₂а₃а₄а₅ (2.8)

Замінивши у виразі (2.8) символи подій а_і їхніми ймовірностями р_і, одержимо рівняння для визначення ймовірності безвідмовної роботи системи

P=p₁p₄+p₂p₅+p₁p₃p₅+p₂p₃p₄-p₁p₂p₃p₄-p₁p₂p₃p₅-2p₁p₂p₄p₅-
-p₂p₃p₄p₅+2p₁p₂p₃p₄p₅ (2.9)

Для системи рівнонадійних елементів (p_i=p) вираз (2.9) легко перетвориться у формулу: P=p⁵+5p⁴q+8p³q²+2p²q³=2p⁵-5p⁴+2p³+2p².

Метод мінімальних шляхів дає точне значення тільки для порівняно простих систем з невеликою кількістю елементів. Для більш складних систем результат розрахунку є нижньою границею ймовірності безвідмовної роботи.

Для розрахунку верхньої границі ймовірності безвідмовної роботи системи можна використовувати метод мінімальних перетинів.

Мінімальним перетином називається набір непрацездатних елементів, відмова яких приводить до відмови системи, а відновлення працездатності кожного з них - до відновлення працездатності системи.

Як і мінімальних шляхів, мінімальних перетинів може бути кілька. Очевидно, система з паралельним з'єднанням елементів має тільки один мінімальний перетин, що включає всі її елементи (відновлення кожного відновить працездатність системи). В системі з послідовним з'єднанням елементів число мінімальних шляхів збігається із числом елементів, і кожний перетин включає один з них.

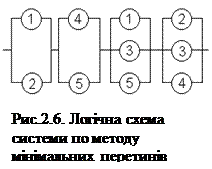В мостиковій системі (рис.2.4, а) мінімальних перетинів чотири (елементи 1 і 2), (4 і 5), (1, 3 і 5), (2, 3 і 4). Логічна схема системи (рис.2.6) складається таким чином, щоб всі елементи кожного мінімального перетину були з'єднані один з одним паралельно, а всі мінімальні перетини - послідовно. Аналогічно методу мінімальних шляхів, складається функція алгебри логіки. “Безвідмовна робота” логічної системи рис.2.6 полягає в “безвідмовній роботі” всіх послідовних ділянок, а “відмова” кожного з них - в одночасній “відмові” всіх паралельно включених елементів. Як видно, оскільки схема методу мінімальних перетинів формулює умови відмови системи, в ній послідовне з'єднання відповідає логічному “АБО”, а паралельне - логічному “І”. Схема рис.2.6 відповідає формулюванню: система відмовить, якщо відмовлять елементи 1 і 2, або 4 і 5, або 1, 3 і 5, або 2, 3 і 4. Функція алгебри логіки запишеться.

(2.10)

Після перетворень із використанням властивостей булевих змінних (2.10) здобуває форму (2.8), після заміни подій їхніми ймовірностями переходить у вираз (2.9).

Таким чином, для мостикової системи з п'яти елементів верхня і нижня границі ймовірності безвідмовної роботи, отримані методами мінімальних перетинів і мінімальних шляхів, збіглися з точними значеннями, отриманими методом прямого перебору. Для складних систем це може не відбутися, тому методи мінімальних шляхів і мінімальних перетинів варто застосовувати спільно.

Дата добавления: 2013-12-14