Предмет математичної фізики. диференціальні рівняння з частинними похідними

Предметом математичної фізики, як відомо [3], є вивчення методів розв’язування задач, що виникають при аналізі широкого класу фізичних явищ, які моделюються диференціальними рівняннями з частинними похідними. Ці рівняння називаються рівняннями математичної фізики. Ми не ставимо перед собою задачу вивчати всі способи розв’язування диференціальних рівнянь з частинними похідними. Розглянемо тільки ті конкретні рівняння, які є дуже важливими для фізики, механіки і техніки.

Зупинимось на основних поняттях таких рівнянь.

Диференціальним рівнянням з частинними похідними відносно невідомої функції 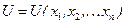називається рівняння, що зв’язує незалежні змінні 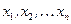, шукану функцію 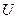та її частинні похідні. Найвищий порядок частинної похідної, що входить в рівняння, називається порядком диференціального рівняння.

Наприклад, 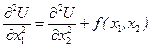– є диференціальним рівнянням з частинними похідними 2-го порядку для функції 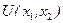класу .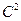

Функція 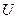називається розв’язком диференціального рівняння з частинними похідними, якщо в результаті підстановки її в рівняння воно перетворюється в тотожність.

Приклад 1.1 Знайти функцію 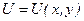, яка є розв’язком диференціального рівняння .

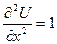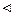Домножимо обидві частини рівняння на 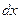і зінтегруємо по змінній :

,

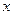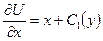де – довільна функція від 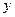(ця функція відіграє роль довільної сталої при інтегруванні по ).

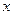Знову домножимо обидві частини рівняння на 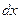та проінтегруємо по :

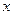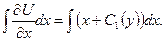
У результаті отримаємо

,

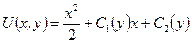де 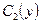– друга довільна функція від .

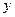Перевіркою легко встановити, що знайдена функція задовольняє задане рівняння, отже, є його розв’язком.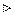

Як бачимо, функція 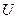залежить від двох довільних двічі диференційовних функцій 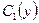та 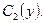У цьому і полягає відмінність розв’язування диференціальних рівнянь з частинними похідними у порівнянні з розв’язуванням диференціальних рівнянь зі звичайними похідними, де розв’язок залежить від довільних сталих. Знайдена функція є загальним розв’язком даного диференціального рівняння з частинними похідними.

Диференціальне рівняння з частинними похідними називається лінійним, якщо шукана функція і всі її частинні похідні входять в рівняння лінійно. Рівняння з частинними похідними називається квазілінійним, якщо воно лінійне відносно всіх старших похідних від невідомої функції.

Диференціальні рівняння математичної фізики, якими ми будемо займатись в подальшому, мають між собою чимало спільного [1]: усі вони – другого порядку, лінійні відносно невідомої функції та її частинних похідних, а коефіцієнти перед функцією та її похідними – сталі числа. Загальний вигляд таких рівнянь для функції 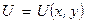є наступним:

,

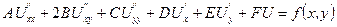де 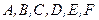– сталі, а права частина – задана функція від .

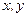Дата добавления: 2013-12-14