Комплексная амплитуда синусоидального тока есть комплексная величина, модуль которой равен амплитуде, а аргумент – начальной фазе данного синусоидального тока

Комплексный мгновенный синусоидальный ток есть комплексная величина, зависящая от времени, модуль и аргумент которой равен соответственно амплитуде и аргументу заданного синусоидального тока.

Литература

1. Попов В.П. Основы теории цепей: Учебник для вузов спец. "Радиотехника".-М.: Высшая школа, 2007 с. 65-95.

1. Основные характеристики гармонических токов

и напряжений

На практике широкое распространение получил переменный ток.

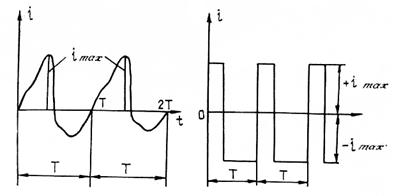
Рисунок 3.1 а, б - Примеры периодических токов

Переменный ток – это ток, значение которого изменяется с течением времени.

Периодический ток – это переменный ток, мгновенное значение которого повторяется через равные промежутки времени. (рис. 3.1 а, б)

Период электрического тока – наименьший интервал времени, по истечении которого значение периодического электрического тока повторяется. Период измеряется в секундах (с). Для периодического тока можно записать:

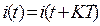
где К – произвольное целое число.

На рисунках 3.1 представлены временные диаграммы тока, т.е. графики зависимости тока от времени.

Частота периодического тока (циклическая) – есть величина, обратная периоду, и характеризующая число периодов в секунду, т.е. скорость завершения полных циклов изменений мгновенных значений периодического тока:

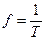
Частота измеряется в герцах (Гц)

Разновидность периодических прочесов, происходящих в радиотехнических цепях, являются гармонические процессы.

Синусоидальным (гармоническим) током называется ток, изменяющийся по синусоидальному или косинусоидальному закону:

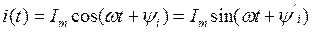_(3.1)

Традиционно в электротехнической литературе используют синусную форму записи гармонического тока(напряжения), а в радиотехнической – косинусную. Обе формы записи являются равноценными, отличаются только началом отсчёта значений и их можно проиллюстрировать одной и той же кривой (рис.3.2).

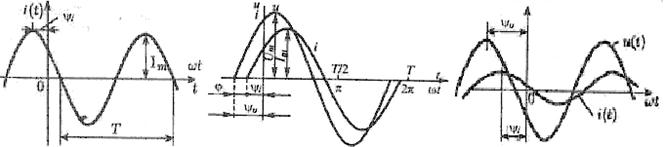
Рисунок 3.2 а, б, в - График гармонического тока и напряжения.

Приведём величины, характеризующие синусоидальный ток:

- амплитуда – наибольшее значение гармонического тока (только для гармонического, в остальных случаях пиковое значение ). Её размерность совпадает с размерностью i(t).

γ(t)=(ωt+ψ_i)- мгновенная фаза (фаза) – аргумент функции i(t);

ω - угловая частота – скорость измерения фазы, выражается в радианах в секунду (рад/с)

Т - период – наименьший временной интервал повторения периодического синусоидального сигнала, т.е. следовательно, ,

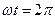откуда период:

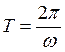
f - циклическая частота – число периодов в секунду, т.е..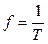

Очевидно, что .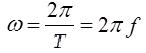

Ток промышленной частоты соответствует f = 50 Гц, а 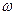=314 рад/с.

- начальная фаза тока определяет значение фазы при t=0 (часть её для удобства записывают в градусах). Она определяет положение ближайшего положительного максимума(в косинусной форме записи) относительно оси координат (рис 2);

при >0 этот максимум будет смещён влево от оси ординат на величину .

разность фаз, или сдвиг по фазе двух синусоидальных функций одинаковой частоты – разность их начальных. Так, если 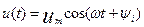, а 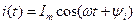, то сдвигом по фазе между током и напряжением называется угол .

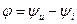Если 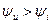, то 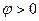(рис 3.2.б), тогда максимум напряжения наступает раньше, чем максимум тока. В этом случае говорят, чтоток отстаёт по фазе на угол 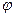от напряжения или напряжение опережает по фазе ток на угол .

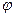Если 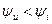, то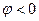, тогда максимум тока наступает раньше, чем максимум напряжения. В этом случае говорят, что ток опережает напряжение на угол 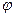или напряжение отстаёт по фазе на угол 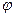от тока.

При 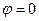имеем , тогда ток и напряжение совпадают по фазе.

Токи и напряжения цепи, изменяющиеся по гармоническому или другому периодическому закону характеризуются средними за период, средневыпрямленными и действующими.

Среднее значение периодического тока за период определяется выражением:

(3.2)

Для гармонически изменяющихся токов и напряжений среднее значение за период равно нулю, так как площадь, ограниченная полуволной и осью времени, равна площади, ограниченной отрицательной полуволной и осью времени. (рис. 3.3)

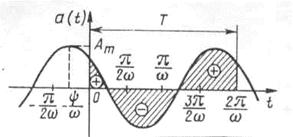
Рисунок 3.3 - К определению понятия среднего значения

периодического тока

Средневыпрямленное значение периодического тока или напряжения называется среднее значение модуля соответствующей периодической функции за период:

Значение пропорционально площади, ограниченной частью кривой и осью времени за период Т, и не зависит от выбора начального момента

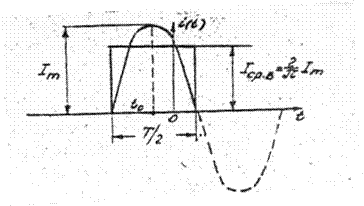
Рисунок 3.4 - К определению понятия средневыпрямленного

значения гармонического тока

Средневыпрямлённое значение гармонического тока или напряжения равно среднему значению соответствующей гармонической функции на положительном полупериоде. (см. рис. 3.4)

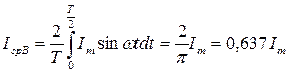(3.3)

Среднее значение за полупериод гармонического тока равно высоте прямоугольника с основанием 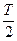, площадь которого равна площади под кривой сигнала

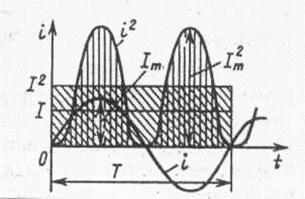
Рисунок 3.5- К определению понятия действующего

значения синусоидального тока

Очень важной характеристикой периодических токов и напряжений являются действующее, или эффективное значение. Действующим значением периодического тока называется среднеквадратическое значение тока за секунду.

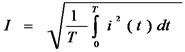(3.4)

Действующее значение I периодического тока i(t)численно равно значению постоянного тока I, при протекании которого за время Т выделяется такое же количество энергии, как и при протекании тока i(t)

Покажем это. Пусть при протекании периодического тока i(t) через линейное сопротивление R в нём в соответствии с выражением (3.4) и законом Джоуля-Ленца за период Т выделяется энергия

(3.5)

Выражение (3.5) совпадает с выражением для энергии, выделяющейся в сопротивлении при протекании через него постоянного тока I_=I в течении времени Т (закон Джоуля-Ленца):

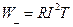
Аналогично можно определить и действующее значение U периодического напряжения и (t).

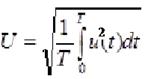(3.6)

Действующее значение I гармонического тока i(t) в 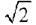раз меньше его амплитуды:

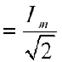(2.7)

Поскольку большинство электроизмерительных приборов реагируют на действующие, а не на максимальные (пиковые)значения токов и напряжений, при описании гармонических и напряжений принято указывать действующее, а не амплитудное значение.

Выражая в (3.1) амплитуду 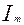через действующее значение I, ещё одну формулу записи гармонического тока:

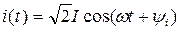(3.8)

В соответствии с ГОСТ 1494-77 обозначают:

мгновенное значение токов и напряжений ветвей, токов источников тока и ЭДС источников напряжения, являющихся гармоническими функциями времени – строчными буквами ;

действующее значение этих величин – соответствующими прописными буквами I, U, J, E

амплитудное значение – теми же прописными буквами с индексом m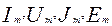

Размерность средних, средневыпрямлённых и действующих значений гармонических токов и напряжений совпадают с размерностью соответствующих функций и, следовательно, с размерностью их амплитуд.

2. Основы метода комплексных амплитуд

2.1 Способы представления гармонических токов.

Понятие о символическом методе

При анализе цепей переменного тока используют следующие способы представления гармонических токов и напряжений:

1) с помощью временных диаграмм.

2) с применением временных диаграмм.

3) с использованием комплексных чисел.

Временная диаграмма гармонического тока i(t) – это график функции времени

Временную диаграмму напряжения можно наблюдать на экране осциллографа.

С помощью временных диаграмм можно производить суммирование и вычитание мгновенных значений токов. (рис. 3.6)

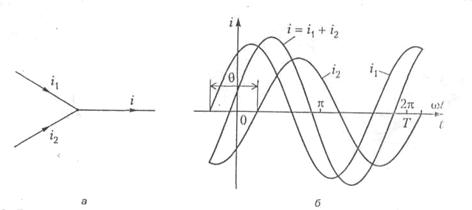
Рисунок 3.6 - Суммирование мгновенных значений токов

на временной диаграмме.

Однако получение суммарного и разностного тока по времени диаграмме является наглядной, но очень трудоёмкой операцией.

Поскольку временная диаграмма периодического тока i(t) представляет собой проекцию вектора, длина которого численно равна амплитуде 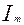, начальное положение на плоскости равно начальной фазе тока, и вращающегося против часовой стрелки с угловой скоростью 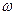(рис. 3.7), то для изображения гармонического тока удобно использовать векторные диаграммы.

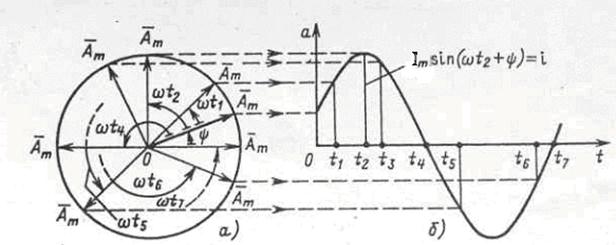
Рисунок 3.7- Представление гармонического тока

вращающимся вектором

При этом рассматриваются не проекции вращающихся с угловой скоростью w векторов, а сами эти векторы.

Векторная диаграмма – это диаграмма представляющая собой совокупность векторов, построенных с соблюдением их взаимной по фазе. Чтобы ‘остановить’ вращение векторов необходимо вращать плоскость вокруг точки начала этих векторов по часовой стрелке с той же угловой частотой 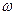, то и предполагается при рассматривании векторных диаграмм.

Векторная диаграмма строится в амплитудных либо в действующих значениях. Отсчёт начальных фаз ведётся от горизонтальной оси. (рис. 3.8)

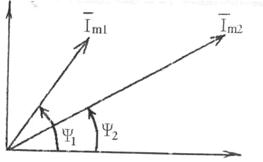
Рисунок 3.8 - Векторная диаграмма токов

По векторной диаграмме можно определить сумму (разность) токов.

Пусть, например,

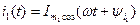
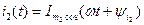
Необходимо найти. Воспользуемся для этого методом векторных диаграмм. Изобразим на плоскости векторы 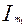и 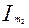со своими начальными фазами. (рис. 3.9)

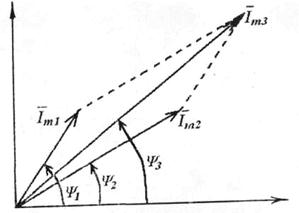
Рисунок 3.9 - Суммирование токов методом векторных диаграмм.

Амплитуда тока находится из векторной диаграмме путём геометрического сложения векторов 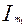и 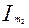. Отсюда же находиться начальная фаза суммарного тока.

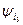Аналогично можно найти и разность токов, используя геометрические построения.

Существенные недостатки метода векторных диаграмм и метода временных диаграмм являются:

недостаточная точность;

большой объём графических работ (громоздкость).

Эти недостатки особенно проявляются при анализе сложных радиотехнических цепей.

Для расчёта сложной цепи гармонического тока, если все источники ЭДС этой цепи генерируют колебания одной и той же частоты, широко применяется метод комплексных амплитуд (иначе – символический или комплексный).

Этот метод разработан в конце XIX века американскими инженерами Ч.П.Штейнметцем и А.Е.Кеннели.

Метод комплексных амплитуд, подобно логарифмическому методу, основан на идее функционального преобразования, при котором операции над исходными функциями (оригиналами) заменяются более простыми операциями над некоторыми новыми функциями, так называемыми изображениями исходных функций. Поэтому методы такого типа называются символическими.

Решение любой задачи символическими методами содержит следующие основные этапы:

- прямое преобразование, в результате которого осуществляется переход от исходных величин (оригиналов) к их символическим (изображениям);

- определение изображений искомых величин путём выполнения по специально установленным правилам операций над изображениями;

- обратное преобразование, с помощью которого переходят от изображений искомых величин к их оригиналам.

Очевидно, что эффективность символического метода определяется трудоемкостью прямого и обратного функциональных преобразований и тем, насколько операции над изображениями проще соответствующих им операций над оригиналами.

Символический метод комплексных амплитуд (комплексный метод) основан на представлении гармонических функций времени в виде комплексных чисел, т.е. на преобразовании исходных функций из временной области (области вещественных переменных) в частотную (область мнимого аргумента jw)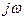

При использовании комплексного метода алгебраически интерпретируется векторная диаграмма.

3.2 Комплексные числа и основные операции над ними

Комплексным числом A называется выражение вида

А = a + jb, (3.9)

где а – действительное число, называемое вещественной составляющей комплексной;

b – действительное число, называемое мнимой составляющей комплексного числа;

– мнимая единица.

Вещественная и мнимая составляющие комплексного числа обозначаются так: ,

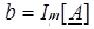
Выражение (3.9) – это алгебраическая форма записи комплексного числа.

Комплексное число А изображается на комплексной плоскости в виде точки А, абсцисса которой равна а, а ордината – b (рис. 3.10 а)

Ось абсцисс, на которой откладывается вещественная часть комплексного числа, называется действительной (Re); ось ординат, на которой откладывается мнимая часть – мнимой ().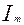

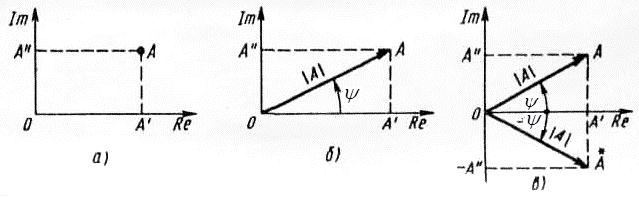
Рисунок 3.10 а, б, в - К определению понятия комплексного числа

Каждой точке А комплексной плоскости и, следовательно, каждому комплексному числу А можно поставить в соответствие вектор А, проведённый из начала координат в точку А. (рис 3.10 б)

Длину вектора, изображающего комплексное число, называют модулем этого числа:

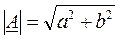(3.10)

Угол между вектором А и положительным направлением вещественной оси называют аргументом комплексного числа:

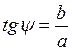(3.11)

Положительное направление отсчёта – против часовой стрелки. Главное значение в промежутке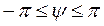

Как видно из рис. 3.11, вещественная а и мнимая b части комплексного числа А есть проекция вектора А на действительную и мнимую оси

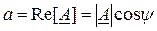
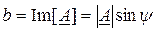(3.12)

Подставляем соотношение (3.12) в выражение (3.9), можно перейти от алгебраической формы записи комплексного числа к тригонометрической:

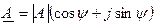(3.13)

Использую форму Эйлера

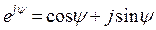(3.14)

где e – основание натурального логарифма, получаем показательную формулу записи комплексного числа:

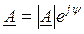(3.15)

Комплексные числа 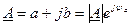и 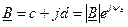считаются равными, если попарно равны их действительные и мнимые части a=c, b=d, или равны их модули | А |=| В |, а аргументы отличаются на 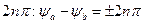,(n – целое число).

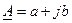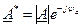Два комплексных числа и называются сопряжёнными, если их действительные части равны а мнимые отличаются только знаком.

Точки на плоскости, изображающие сопряжённые комплексные числа, симметричны относительно действительной оси (рис. 3.10 в)

Модули сопряжённых чисел равны, а главные значения их аргументов отличаются только знаком:

Арифметические операции над комплексными числами выполняются так же, как над обыкновенными двучленами, учитывая что ,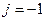

Операции сложения и вычитания удобнее выполнять, используя алгебраическую форму записи:

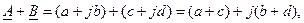(3.16)

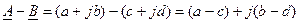
сумма двух сопряжённых комплексных чисел 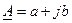и 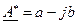представляет собой действительное число.

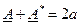(3.17)

Умножение, деление и возведение в степень комплексных чисел удобнее производить в показательной форме:

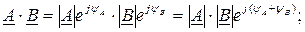
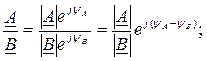(3.18)

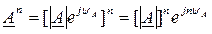
Из выражений(3.18) следует, что при умножении вектора 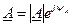на действительное число m получается новый вектор, модуль которого в m раз больше модуля А: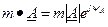

При умножении вектора 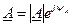на вектор 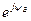, модуль которого равен единице, образуется новый вектор, повёрнутый относительно вектора А на угол против часовой стрелки:

(3.19)

Из выражения (3.19) и формулы Эйлера (3.14) также, что умножение вектора 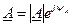на вектор

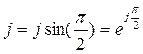(3.20)

равносильно повороту вектора А на угол против часовой стрелки:

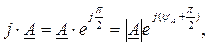
а умножение вектора А на вектор приводит к повороту вектора А на угол по часовой стрелке:

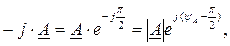
Умножение вектора А на равносильно изменению аргумента А на: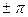

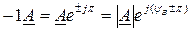
2.3. Представление гармонических токов и напряжений

в комплексной форме

При использовании метода комплексных амплитуд необходимо уметь записывать символы (комплексные числа), характеризующие функции мгновенных значений электрических величин, их амплитуды и действующие значения.

Рассмотрим этот вопрос применительно к синусоидальному току:

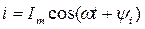
Ранее было доказано, что этой функции соответствует вектор 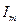, вращающийся против часовой стрелки с угловой скоростью 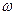равной угловой частоте тока (рис. 3.11 а).

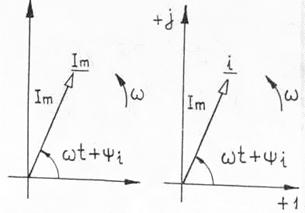
Рисунок 3.11 а, б - Соответствие вращающемуся вектору (а)

комплексного числа (б)

Комплексный мгновенный ток. Вращающемуся вектору тока 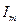, помещённому на комплексную плоскость (рис.3.11 б) соответствует комплексное число

(3.22)

Данное комплексное число i можно принять в качестве символа мгновенного синусоидального тока, при этом:

(3.23)

– его вещественная составляющая,

(3.24)

– его мнимая составляющая.

Комплексное число i (3.22) в теории цепей принимается в качестве символа функции времени мгновенного синусоидального тока при условии, что мнимая часть 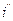этого комплекса (3.24) вообще опускается при переходе от символа к оригиналу. Таким образом, символом функции времени мгновенного синусоидального тока i(t) является комплексное число i, называемое комплексным мгновенным синусоидальным током.

Из соотношения для 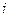(3.22) следует определение этого тока:

Комплексная амплитуда тока. Если рассмотреть вращающийся вектор синусоидального тока (рис. 3.11 а) в момент времени t =0, т.е. в момент начала отсчёта (рис. 3.12 а), то этот вектор можно считать неподвижным. На комплексной плоскости этому вектору соответствует число 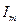, называемое комплексной амплитудой данного синусоидального тока:

(3.25)

Комплексная амплитуда 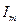является частью комплексного мгновенного тока.

Действительно, с углом (3.22) и (3.25) можно записать:

(3.26)

Множитель (оператор вращения) характеризует зависимость комплексного мгновенного тока i от времени. В комплексной амплитуде тока (3.25) он отсутствует.

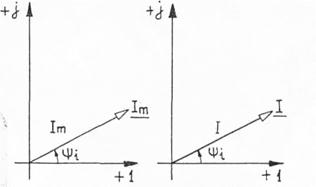
Рисунок 3.12 а, б - Комплексная амплитуда тока(а)

и комплексный действующий ток.

Комплексный действующий ток. Большинство расчётных соотношений для цепей гармонических токов записываются через действующие значения электрических величин (тока, напряжения, ЭДС). Переход к символической форме записи требует выбора символа (комплексного числа) и для действующих значений электрических величин.

Применительно к синусоидальному току символ действующего значения тока можно получить делением комплексной амплитуды тока (3.25) на

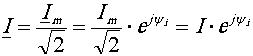(3.27)

Данному комплексному числу соответствует неподвижный вектор, как и комплексному числу 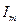, но уменьшенный по длине в (рис. 3.12 б).

Это комплексное число (2.27) называется комплексным действующим током.

Дата добавления: 2013-12-14