
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Геометрической сумме векторов синусоидальных электрических величин соответствует алгебраическая сумма комплексных чисел, изображающих эти векторы
|
|
|
|
Пример 3. Сложение комплексных чисел изображающих вектора.
Комплексный действующий синусоидальный ток (комплексный ток) есть комплексная величина, модуль которой равен действующему значению синусоидального тока, а аргумент – начальной фазе этого тока.
Пример 1. Пусть имеется гармонический ток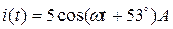
Тогда комплекс мгновенного тока: 
Комплексная амплитуда тока:
 – в показательной форме;
– в показательной форме;
 – в тригонометрической форме;
– в тригонометрической форме;
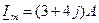 – в алгебраической форме.
– в алгебраической форме.
Комплексный действующий ток:
 – в показательной форме;
– в показательной форме;
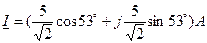 – в тригонометрической форме;
– в тригонометрической форме;
 – в алгебраической форме.
– в алгебраической форме.
Вещественная часть комплекса мгновенного тока есть исходный гармонический ток:
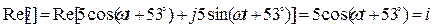
Пример 2. Напряжению  соответствует комплексная амплитуда
соответствует комплексная амплитуда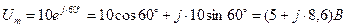
2.4 Операции над комплексными изображениями
гармонических функций
Комплексный метод предполагает замену геометрических операций над векторами синусоидальных электрических величин алгебраическими операциями над их символами (комплексными числами).

Рисунок 3.13 а, б, в - Сложение комплексных токов.
Покажем возможность такой алгебраизации геометрических задач на следующем примере.
В цепи синусоидального тока, изображённой на рис. 2.13 а, действующее значение тока суммируется геометрически, что подтверждает векторная диаграмма токов для данной цепи (рис 3.13 б), т.е.
 (3.28)
(3.28)
При этом проекция результирующего вектора 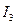 на соответствующие оси системы координат равны сумме проекций составляющих векторов
на соответствующие оси системы координат равны сумме проекций составляющих векторов  и
и  на этой же оси.
на этой же оси.
 ;
; 
Векторной диаграмме токов, помещённой на комплексную плоскость (рис. 3.13 в) соответствует система чисел  ,
,  ,
, 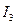 , являющихся символами рассматриваемых векторов токов:
, являющихся символами рассматриваемых векторов токов:
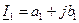 ;
; 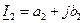 ;
; 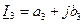 (3.29)
(3.29)
Символами результирующего вектора 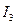 с учётом соотношений (3.29) можно записать следующим образом:
с учётом соотношений (3.29) можно записать следующим образом:
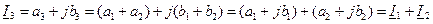 , т.е.
, т.е.
 (3.30)
(3.30)
Сравнивая выражения (3.28) и (3.30) можно сделать вывод о соответствии геометрических и алгебраических операций.
Распространяя этот результат на все аналогичные линейные операции над гармоническими функциями времени, можно сделать вывод, что любые геометрические операции над векторами синусоидальных электрических величин можно заменить алгебраическими операциями над символами этих величин, в качестве которых используются комплексные числа. Другими словами линейным операциям над гармоническими функциями времени соответствуют линейные операции над их комплексами.
В лекции №1 показано, что для расчёта последовательной RLC-цепи необходимо решить следующее интегро-дифференциальное уравнение, составленное на основе второго закона Кирхгофа:
Решение этого уравнения сопряжено с выполнение операций дифференцирования и интегрирования функций времени.
Применение комплексного метода позволяет решать подобные уравнения более простым алгебраическим способом.
Рассмотрим это подробнее. Пусть ток в цепи изменяется по синусоидальному закону
Тогда его производная и интеграл соответственно записываются следующим образом:
 (3.31)
(3.31)
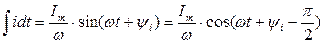 (3.32)
(3.32)
Новым синусоидальным функциям (3.31) и (3.32) соответствуют свои мгновенные комплексные значения(символы), которые по аналогии с соотношением (3.26) можно записать так:

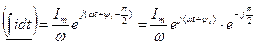 .
.
С учётом формул (3.20), (3.21) и (3.26) окончательно получим:
 (3.33)
(3.33)
 (3.34)
(3.34)
Комплексные числа (3.33) и (3.34) являются символами производной и интеграла синусоидальных функций электрических величин и отражают смысл алгебраизации операций дифференцирования (интегрирования) оригиналов:
Операции дифференцирования (интегрирования) синусоидальных функций можно заменить алгебраическими операциями умножения (деления)комплексных мгновенных значений (комплексных амплитуд) этих функций на 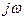 .
.
|
|
|
Дата добавления: 2013-12-14; Просмотров: 597; Нарушение авторских прав?; Мы поможем в написании вашей работы!