Величина, обратная комплексному сопротивлению, называется комплексной входной проводимостью двухполюсника

Таким образом, при переходе от синусоидальных электрических величин (оригиналов) к их символам (комплексным числам)удаётся полностью алгебраизовать все операции над синусоидальными электрическими величинами.

Это позволяет существенно упростить анализ линейных цепей, находящихся под гармоническим воздействием, т.к. даёт возможность заменить систему интегро-дифференциальных уравнений электрического равновесия цепи, составленную для мгновенных значений токов и напряжений ветвей, системой алгебраических уравнений для комплексных амплитуд соответствующих токов и напряжений.

В этом и заложена основа комплексного метода расчёта гармонических цепей.

3. Комплексное сопротивление пассивного

двухполюсника. Закон Ома в комплексной форме

Рассмотрим произвольный пассивный линейный двухполюсник, находящийся под гармоническим воздействием. (рис. 3.14)

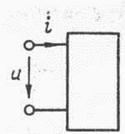
Рисунок 3.14 - Идеализированный пассивный двухполюсник.

Ток 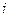и напряжение 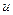на зажимах этого двухполюсника являются гармоническими функциями времени:

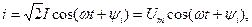
Комплексным входным сопротивлением (комплексным сопротивлением) пассивного двухполюсника называется отношение комплексной амплитуды напряжения на зажимах двухполюсника к комплексной амплитуде тока:

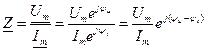(3.35)

Выражая комплексные амплитуды тока и напряжения через соответствующие комплексные действующие значения 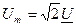; , получим, что комплексное сопротивление пассивного двухполюсника может быть найдено как отношение комплексных действующих значений тока и напряжения:

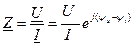(3.36)

Комплексное сопротивление произвольного двухполюсника в общем случае представляет собой комплексное число, поэтому оно может быть представлено в показательной

(3.37)

тригонометрической

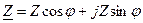(3.38)

или алгебраической

(3.39)

формах.

Величина z =|Z | называется модулем комплексного сопротивления (полным входным сопротивлением) и определяет отношение амплитуды напряжения к амплитуде тока?

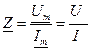(3.40)

Величина 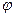называется аргументом комплексного сопротивления и равен разности начальных фаз напряжения и тока:

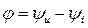(3.41)

В зависимости от фазовых соотношений между напряжением и током значения может быть больше нуля (напряжение опережает ток по фазе), меньше нуля (напряжение отстаёт по фазе от тока) или равно нулю (ток и напряжение совпадают по фазе).

Величина и называется соответственно вещественной (активной или резистивной ) или мнимой (реактивной ) составляющими комплексного сопротивления

Комплексное входное сопротивления может быть представлено в виде вектора, расположенного в комплексной плоскости, длина которого в определённом масштабе равна Z, а угол наклона к положительной вещественной полуоси равен 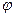(рис 3.15)

Рисунок 3.15 - Изображение комплексного сопротивление

на комплексной плоскости

,

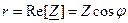Вещественная и мнимая составляющие входного сопротивления представляют собой проекции вектора на вещественную и мнимую оси.

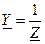(3.42)

Комплексная проводимость определяется как отношение комплексных амплитуд или комплексных действующих значений тока и напряжения на зажимах рассматриваемого двухполюсника:

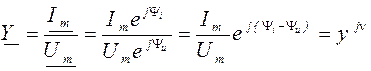(3.43)

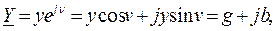
где

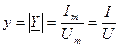- модуль комплексной входной проводимости, называемый полной входной проводимостью двухполюсника и является величиной, обратной модулю комплексного входного сопротивления:

– аргумент входной проводимости равный по абсолютному значению и противоположен по знаку аргументу комплексного входного сопротивления.

g и b – вещественная (резистивная) и мнимая (реактивная) составляющие входной проводимости, которые можно рассматривать как проекции вектора Y на вещественную и мнимую оси положительной плоскости (рис. 3.16):

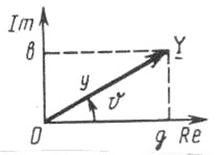
Рисунок 3.16 - Изображение комплексной проводимости

на комплексной плоскости.

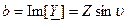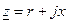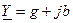Подставляя в (2.42) и определим связь между вещественными и мнимыми составляющими комплексного сопротивления и комплексной проводимости двухполюсника:

(3.44)

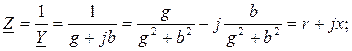(3.45)

Введение понятия комплексного сопротивления, как коэффициента пропорциональности между комплексной амплитудой напряжения и комплексной амплитудой тока, и означает введение закона Ома в комплексной форме:

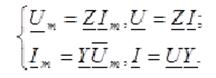(3.46)

По форме записи закон Ома в комплексной форме (3.46) аналогичен закону Ома для резистивной цепи, однако, здесь он устанавливает связь не между током и напряжением двухполюсника, а между комплексными амплитудами синусоидального тока и напряжения двухполюсника.

4. Комплексная схема замещения цепи. Законы Кирхгофа

в комплексной форме

На основе закона Ома в комплексной форме каждому участку линейной электрической цепи, составленного из идеализированных пассивных элементов и имеющему два внешних вывода(рис. 3.16), т.е. идеализированному пассивному двухполюснику можно поставить в соответствие комплексную схему замещения, на которой рассматриваемый участок цепи представлен комплексным сопротивлением или проводимостью, а токи или напряжения на его зажимах – комплексными амплитудами (рис. 3.17 а) или комплексными действующими значениями. (рис. 3.17 б)

Рисунок 3.17 - Комплексные схемы замещения идеализированного

пассивного двухполюсника

Представляя все входящие в моделирующую цепь идеализированные пассивные элементы их комплексными схемами замещения, а токи и ЭДС идеализированных источников – их комплексными амплитудами или действующими значениями, получаем комплексную схему замещения цепи (схему замещения для комплексных амплитуд или схему замещения для комплексных действующих значений).

Дата добавления: 2013-12-14