Сумма комплексных ЭДС, действующих в замкнутом контуре электрической цепи, равна сумме комплексных падений напряжений на комплексных сопротивлениях участков этого контура

Таким образом, комплексная схема замещения цепи может быть получена из схемы замещения для мгновенных значений заменой всех идеализированных пассивных двухполюсников их комплексными сопротивлениями (проводимостями) и всех токов и напряжений – их комплексными изображениями.

По внешнему виду комплексная схема замещения цепи постоянного тока, составленная только из сопротивлений и идеализированных источников энергии, причем, подобно цепи постоянного тока, компонентные уравнения всех ветвей в комплексной форме являются алгебраическими.

Мгновенное значение токов и напряжений различных ветвей электрической цепи связаны между собой линейными алгебраическими уравнениями баланса токов и напряжений, составляемые на основании закона Кирхгофа.

Учитывая, что суммированию гармонических функций времени соответствует суммирование их комплексных изображений, перейдём от законов Кирхгофа для мгновенных значений токов и напряжений и законов Кирхгофа для комплексных изображений токов и напряжений, называемых законами Кирхгофа в комплексной форме.

Первый закон Кирхгофа в комплексной форме устанавливает связь между комплексными изображениями токов в каждом из узлов моделирующей цепи:

Сумма комплексных амплитуд (комплексных действующих значений) токов всех ветвей, подключённых к каждому из узлов электрической цепи, равна нулю:

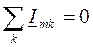, (3.47)

где k – номер ветви, подключённой к рассматриваемому узлу.

Второй закон Кирхгофа в комплексной форме определить связь между комплексными изображениями напряжений ветвей, входящих в произвольный контур электрической цепи:

Сумма комплексных амплитуд (комплексных действующих значений) напряжений всех ветвей, входящих в замкнутый контур электрической цепи, равна нулю:

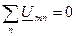, , (3.48)

где n – номер ветви, входящий в рассматриваемый контур.

В ряде случаев удобно использовать другую формулировку второго закона Кирхгофа в комплексной форме:

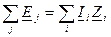(3.49)

Закон Кирхгофа сформулирован только для мгновенных значений, комплексных амплитуд и комплексных мгновенных значений токов и напряжений.

Они не выполняются для амплитуд и действующих значений соответствующих величин.

Используя выражения для законов Ома и Кирхгофа в комплексной форме, можно составить систему уравнений электрического равновесия цепи для комплексных изображений токов и напряжений. В отличие от системы уравнений электрического равновесия для мгновенных значений токов и напряжений уравнения электрического равновесия для комплексных изображений токов и напряжений являются алгебраическими. Решение таких уравнений намного проще, чем решение дифференциальных уравнений электрического равновесия, составленных для мгновенных значений токов и напряжений.

Дата добавления: 2013-12-14