Алгоритм анализа цепи методом комплексных амплитуд

1. Переход от гармонических токов и напряжений всех ветвей к их комплексным изображениям (комплексным амплитудам или комплексным действующим значениям).

2. Переход от схемы замещения цепи для мгновенных значений к комплексной форме замещения.

3. Составление уравнений электрического равновесия цепи для комплексных изображений токов и напряжений но основе законов Ома и Кирхгофа в комплексной форме.

4. Решение системы уравнений электрического равновесия относительно комплексных изображений интересующих токов и напряжений.

5. Переход от комплексных изображений интегрирующих токов и напряжений к их оригиналам.

5. Идеализированные пассивные элементы

при гармоническом воздействии

5.1 Резистивный элемент.

Пусть к резистивному элементу (рис. 3.20)

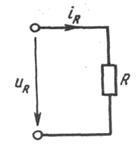
Рисунок 3.20 - Резистивный элемент

Приложено напряжение, изменяющееся по гармоническому закону (рис.3.21,а):

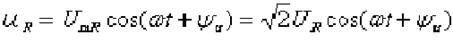(3.50)

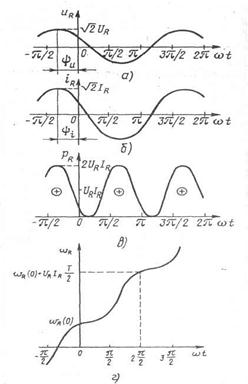
Рисунок 3.21, а, б, в, г - Временные диаграммы (а) напряжения, (б) тока,

мгновенной мощности (в) и энергии (г) резистивного элемента.

Определим ток резистивного элемента 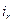и его комплексное входное сопротивление 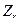, а также построим диаграммы, характеризующие зависимость тока, напряжения и мгновенной мощности от времени.

Связь между мгновенными значениями тока и напряжения линейного резистивного элемента определяется.

Подставляя (3.50) в выражение для закона Ома, находим

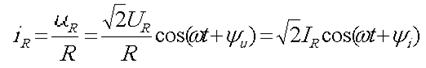(3.51)

Анализ выражения (3.51) позволяет сделать следующие выводы.

При гармоническом внешнем воздействии ток резистивного элемента является функцией времени той же части, что и напряжение (рис. 3.21 б):

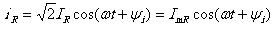
Ток и напряжение линейного резистивного элемента совпадают по фазе:

(3.52)

Действующие значения напряжения и тока связаны между собой отношением:

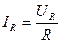, (3.53)

подобный закону Ома для мгновенных значений.

Комплексный ток и напряжение резистивного элемента:

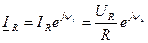и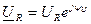

На комплексной плоскости напряжение 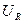и ток изображаются векторами, которые совпадают по направлению и различаются только масштабом (рис.3.22,а).

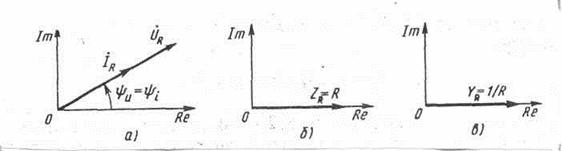
Рисунок 2.22 а, б, в - Векторная диаграмма тока и напряжения, комплексного

сопротивления, и комплексной проводимости резистивного элемента.

Комплексное сопротивление 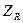резистивного элемента равно отношению комплексных действующих значений напряжения и тока:

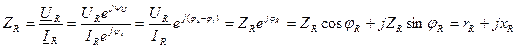(3.54)

Анализ выражения (3.54) с учётом (3.52) и (3.53) позволяет сделать следующие выводы:

1. Модуль комплексного сопротивления;

;

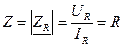2. Аргумент комплексного сопротивления;

;

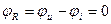3. Комплексное входное сопротивление резистивного элемента содержит только вещественную составляющую:

,

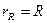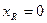
На комплексной плоскости комплексное сопротивление изображается вектором, направленным вдоль вещественной оси (рис. 3.22 б).

Комплексная проводимость резистивного элемента по аналогии (3.54) будет иметь вид:

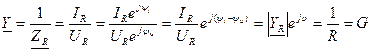(3.55)

Комплексная проводимость резистивного элемента также изображается вектором, направление которого совпадает с направлением положительной вещественной полуоси (рис.3.22, в).

Комплексная схема замещения резистивного элемента (рис. 3.23) имеет такой же вид, как и схема замещения этого элемента для мгновенных значений (рис. 3.20), и отличается от последней только тем, что мгновенные значения тока 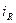и напряжения 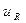заменены их комплексными изображениям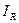и и .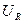

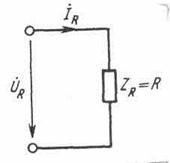
Рисунок 3.23 - Комплексная схема замещения участка цепи,

содержащего резистивный элемент

Мгновенная мощность резистивного элемента определяется произведением мгновенных значений напряжения 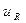и тока :

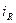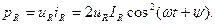
С учётом того, что 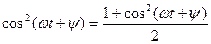, мгновенную мощность резистивного элемента можно представить в виде:

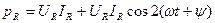(3.56)

Из выражения (3.56) следует, что мгновенная мощность резистивного элемента содержит две составляющие:

- постоянную, равная произведению действующих значений тока и напряжения;

- переменную, изменяющуюся во времени по гармоническому закону с частотой, удвоенной по сравнению с частотой воздействующего напряжения (рис. 3.21,в).

Максимальное значение мощности резистивного элемента равно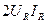, а минимальное – нулю.

Выводы:

Дата добавления: 2013-12-14