Полоса пропускания контура

При передачи музыки, речи или телевизионного сигнала требуется определенная полоса частот. Амплитудно-частотная характеристика является сложной функцией расстройки, поэтому для ориентировочных расчетов ее заменяют идеальной характеристикой, имеющей вид прямоугольника с высотой, равной 1 (рис.7.5).

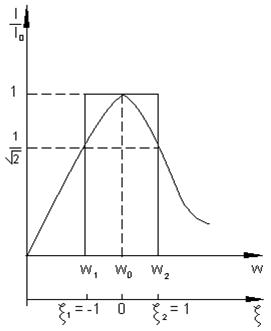
Рисунок 7.5 – Замена АЧХ идеальной АЧХ

Ширина этого прямоугольника по оси часто называется полосой пропускания. Абсолютной полосой пропускания называется величина

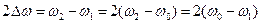(7.29)

где – нижняя и 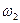– верхняя граничные частоты полосы пропускания;

.

Относительной полосой пропускания называется величина

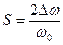(7.30)

Границы полосы пропускания частот являются величиной условной.

Граничная частота – это та частота, при которой средняя мощность, поглощаемая последовательным контуром, вдвое меньше средней мощности, поглощаемой при резонансе:

,

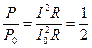т.е. полагается, что все колебания, мощность которых уменьшается не более, чем в два раза, контуром пропускаются, а все остальные колебания контуром подавляются. При уменьшении мощности в два раза ток должен уменьшаться в 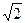раза:

(7.31)

Полоса пропускания последовательного колебательного контура – это диапазон частот, в пределах которого значение АЧХ составляют не менее, чем 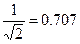ее максимального значения на резонансной частоте (рис. 7.5).

Из выражения (7.31) следует, что на границе полосы пропускания должны выполняться условия:

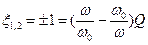
Причем для нижней граничной частоты 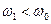соответствует уравнение:

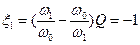(7.32)

а для верхней граничной частоты 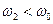соответствует уравнение:

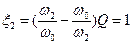(7.33)

Решая уравнения (7.32) и (7.33) для положительных корней, получим выражение для гармонических частот:

(7.34)

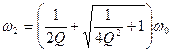
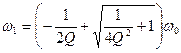
Тогда полоса пропускания равна:

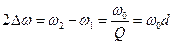, (7.35)

а относительная полоса пропускания равна:

(7.36)

Таким образом, полоса пропускания, характеризующая избирательные свойства колебательного контура, пропорциональна резонансной частоте и обратно пропорциональна добротности; относительная полоса пропускания равна затуханию контура.

Полоса пропускания только приближенно характеризует избирательные свойства контура, но для большинства расчетов точность оказывается вполне достаточной. Для некоторых специальных расчетов, например, для оценки электромагнитной совместимости устройств, учитывают реальные формы АЧХ.

4. Резонанс в параллельном колебательном контуре

Дата добавления: 2013-12-14