Условия возбуждения резонанса токов

Резонансом токов называется явление резонанса в участке электрической цепи, содержащей параллельно соединенные индуктивный и емкостной элементы.

В реальной цепи конденсатор имеет потери в диэлектрике, а активное сопротивление обмотки катушки индуктивности может быть значительным, поэтому анализ режима резонанса необходимо проводить на основе схемы замещения цепи, изображенной на рис.7.6. На данной схеме в ветвях с реактивными элементами последовательно внесены резисторы с сопротивлениями R₁ и R₂.

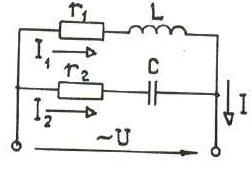
Рисунок 7.6

Параллельным колебательным контуром называется электрическая цепь, в которой индуктивность и емкость включены параллельно источнику напряжения.

Рассмотрим проводимость первой ветви с индуктивностью:

Y ₁ = 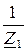= = 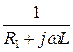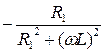- j 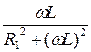= g ₁ + jb ₁, (7.37)

где g₁ = 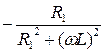- активная проводимость первой цепи (7.38)

b ₁ = - реактивная индуктивная проводимость первой ветви.

Рассмотрим проводимость второй ветви с конденсатором:

Y ₂ = 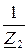= = 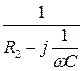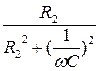- 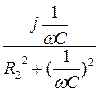= g ₂ + jb ₂, (7.39)

где g ₂=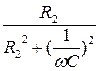- активная проводимость второй ветви; (7.40)

b ₂ = 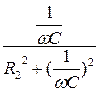- реактивная (емкостная) проводимость второй ветви. (7.41)

По определению резонансного режима ток I должен совпадать по фазе с напряжением U, т.е. φ = ψ_U – ψ_I = 0. Это будет и при условии, что сумма реактивных проводимостей ветвей равна нулю:

b ₁ + b ₂ = 0 (7.41)

Следовательно, условием возбуждения резонанса токов является равенство индуктивной и емкостной проводимостей:

b ₀₁ = b ₀₂; 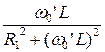=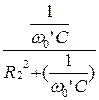, (7.42)

где 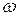₀' - угловая резонансная частота при резонансе токов.

Резонансная частота и способы возбуждения резонанса токов. Резонансную угловую частоту можно получить из соотношения (7.42), разрешив его относительно 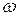₀':

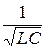
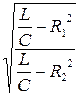ω₀'==₀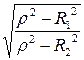, (7.43)

где 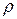= 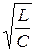- волновое сопротивление цепи;

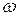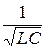₀ = - угловая частота, при которой имеет место резонанс напряжений при последовательном соединении конденсатора и катушки.

Анализ формулы (7.43) свидетельствует, что резонанс токов возможен при выполнении следующих условий вещественности 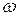₀':

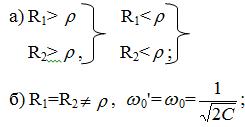
т.е. ω₀' - величина неопределенная; физически это означает, что резонанс возможен при любой частоте.

При соотношении параметров R₁ < 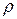< R₂ или R₂ < 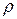< R₁ резонанса токов в цепи не будет ни при какой частоте.

Формула (7.43) свидетельствует, что резонанса токов можно добиться теми же способами, которыми обеспечивается резонанс напряжений: изменением частоты приложенного к цепи напряжения 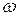или собственной резонансной частоты 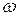₀', т.е. на основе равенства 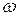=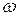₀'.

Дата добавления: 2013-12-14