Линейная зависимость, размерность и базис в линейном пространстве

Определение.

1°. Выражение 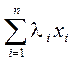называется линейной комбинацией элементов 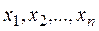линейного пространства R.

2°. Элементы 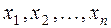линейного пространства R называются линейно зависимыми, если существуют числа 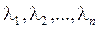, не равные нулю одновременно, такие, что .

3°. Элементы 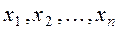линейного пространства R называются линейно независимыми, если из равенства следует, что .

Лемма 13.1 Для того чтобы некоторое множество элементов линейного пространства было линейно зависимым, необходимо и достаточно, чтобы один из этих элементов являлся линейной комбинацией остальных.

Доказательство.

Доказательство дословно совпадает с доказательством леммы 1 из первой лекции, в котором слово “вектор” следует заменить словом “элемент”.

Лемма 13.2 Если некоторое подмножество элементов линейно зависимо, то линейно зависимы и сами элементы .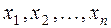

Доказательство.

Без ограничения общности можно предположить, что линейно зависимое подмножество состоит их первых 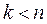элементов множества 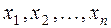. Тогда существуют не равные нулю одновременно числа , такие, что 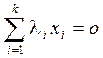. Но из этого соотношения вытекает равенство 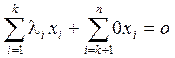, которое означает линейную зависимость элементов .

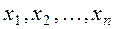Лемма доказана.

Определение. Базисом в линейном пространстве R называется любой упорядоченный набор его n элементов, если

(1). эти элементы линейно независимые;

(2). любое подмножество в R, содержащее 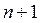элемент, включая эти n элементов, линейно зависимо.

Определение. Линейное пространство R называется n - мерным и обозначается 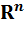, если в нем существует базис, состоящий из n элементов. Число n называется размерностью линейного пространства 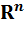и обозначается .

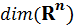Теорема 13.4 Для каждого элемента линейного пространства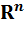существует единственное представление в виде линейной комбинации базисных элементов.

Доказательство.

Пусть в линейном пространстве 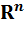заданы базис 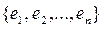и произвольный элемент x. Тогда, по определению базиса, система элементов 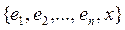линейно зависима и по лемме 13.1 элемент x является линейной комбинацией элементов . Существование разложения таким образом доказано.

Покажем теперь единственность разложения. Допустим, что существуют две различные линейные комбинаци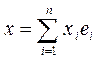и и 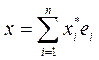. Тогда получаем, что

,

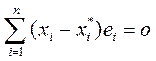но это означает, что при данном допущении система элементов 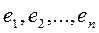линейно зависима. Полученное противоречие доказывает единственность.

Теорема доказана.

В общем случае линейное пространство может не иметь базиса. Таким свойством обладает, например, линейное пространство, состоящее из одного нулевого элемента.

В таблице приведены примеры базисов в линейных пространствах.

Дата добавления: 2013-12-13