Модель парной линейной регрессии

VII. Оценки

VI. Мода.

Мода – это число, делящее выборку пополам, т.е. 50% значений лежит выше нее, а 50% - ниже. Обозначается mod.

Пример:

Медиана показывает насколько справедливо среднее.

Введем обозначения:

истинное значение параметра

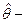оценка параметра

Т.к. истинное значение параметра неизвестно, то мы его находим (оцениваем) по некоторой выборке объема Т.

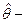то число, которое скорее всего примет истинное значение.

Свойства оценок:

Мы стараемся найти и подобрать выборку таким образом, чтобы по ней получить оценки, которые:

1) состоятельны, т.е. при оценка стремится к истинному значению, т.е., чем больше выборка, тем точнее оценка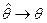

2) несмещенность, т.е. математическое ожидание оценки – это истинное значение, т.е. в среднем мы получаем истинное значение

3) эффективность, т.е. дисперсия оценки – минимальна

Замечание: дисперсия напрямую связана с точностью оценивания. Чем выше дисперсия, тем больше варьируемость признака, тем менее точный результат мы получаем.

Пусть Y,X – две выборки объема Т.

Возникает вопрос. Связаны ли они между собой? Если да, то как, и как выразить эту связь количественно?

У

Х

Необходимо подобрать а и bтакими, чтобы линия была как можно ближе ко всем значениям. a иb – неизвестные параметры. Необходимо подобрать a иb, минимизировав меру расстояния от точек, до получившейся прямой. В качестве меры можно взять сумму квадратов отклонения от среднего

Т.е. мы суммируем квадраты расстояния в каждой точке между наблюдаемым значением и тем, что лежит на линии. Берется квадрат расстояний, чтобы большим расстояниям придать больший вес, а также избежать отрицательных значений.

Иногда в качестве меры отклонения берут модуль расстояния

Но вычисления с модулем гораздо сложнее. Мы будем использовать квадрат отклонений.

Для нахождения неизвестных параметров а и b, имея в распоряжении выборки Y и X объема Т, нам необходимо минимизировать следующее расстояние

Мы ищем линию, которая будет максимально близко лежать от этих точек.

Применяя метод Лагранжа в решении подобных задач, получаем что:

,

где

Мы получили оценки неизвестных параметров a и b, удовлетворяющие свойствам оценок, с помощью которых можно построить уравнение регрессии и найти качественную зависимость между X и Y.

, ,

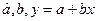
- вектор из двух букв a и b.

В данном случае построить регрессию, значит найти оценку вектора .

- матричная форма записи

Дата добавления: 2013-12-13