Ширина класового інтервалу(крок), частоти класових інтервалів

ІНТЕРВАЛЬНІ СТАТИСТИЧНІ РОЗПОДІЛИ

Інтервальний статистичний розподіл вибірки та його побудова за дискретним статистичним розподілом, класові інтервали, формула Стерджеса,

Коли ознака варіює в широких межах, і кількість статистичних даних велика то, вихідні дані групують у так звані класові інтервали, які містять в собі дані які можна вважати близькими у відповідності з величиною вибірки та масштабами даних.

Кількість класових інтервалів 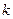визначається за формулою Стерджеса:

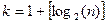, де 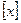- ціла частина числа .

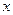Оскільки 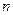в більшості випадків є степінь числа 10, то формулу Стерджеса записують також у вигляді: .

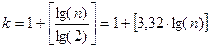Ширину класового інтервалу (крок) 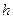визначають за формулою 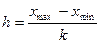, де 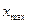- максимальне значення варіюючої ознаки; 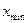- мінімальне значення варіюючої ознаки;

На практиці з метою збереження більш повної інформації про явище, що досліджується, побудова класових інтервалів, починається не з 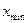, а закінчується не 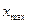, а визначається величинами 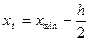(х початкове), 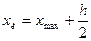(х кінцеве).

Розбиття на класові інтервали робиться для проміжку 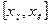на відрізки 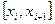довжина яких дорівнює кроку, тобто , .

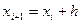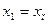Оскільки розширення проміжку 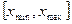до проміжку 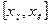збільшує довжину першого на величину 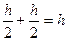то фактична кількість класових інтервалів в практичних задачах є більшою на одинцю ніж за формулою Стерджеса.

Частотою класового інтервалу називають кількість елементів вибірки які попадають в цей інтервал. Частоту яка відповідає інтервалу 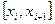позначають .

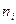Інтервальним статистичним розподілом вибірки називають таблицю яка складається з двох рядків, в першому рядку вказують сукупність інтервалів, а в другому рядку сукупність відповідних їм частот.

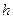
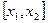
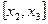
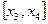
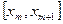
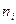
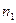
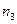
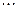
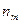
Зауваження В більшості випадків числа 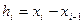, (які є довжинами відповідних інтервалів), є однаковими, але існують задачі в яких ці величини різні.

Дата добавления: 2013-12-13