КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Класифікація точкових оцінок
|
|
|
|
Означення точкової статистичної оцінки.
ТОЧКОВІ СТАТИСТИЧНІ ОЦІНКИ
Поняття статистичної оцінки.
СТАТИСТИЧНІ ОЦІНКИ
Параметри генеральної сукупності є величинами сталими, але їх числове значення невідоме. Ці параметри оцінюються параметрами вибірки.
Якщо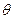 
параметр генеральної сукупності, відповідну йому статистичну оцінку позначають 
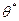. При цьому 
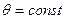, а 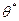випадкова величина, що має певний закон розподілу ймовірностей.
Статистична оцінка яка визначається одним числом, називається точковою статистичною оцінкою.
Точкова оцінка називається незміщеною якщо її математичне сподівання дорівнює параметру, що оцінюється: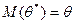 
Нехай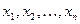 
вибірка з досліджуваної генеральної сукупності з параметром 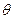, через 
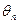позначимо точкову оцінку яка визначається цією вибіркою.
Точкова оцінка називається обгрунтованою якщо вона збігається по ймовірності до оцінюваного параметра тобто: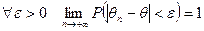 
.
Оцінки, які мають властивості незміщеності та обґрунтованості можуть відрізнятися дисперсіями.
Точкова оцінка називається ефективною якщо вона має мінімальну дисперсію.
|
|
|
Дата добавления: 2013-12-13; Просмотров: 337; Нарушение авторских прав?; Мы поможем в написании вашей работы!