Оцінки одержані методом найбільшої правдоподібності завжди обґрунтовані, ефективні але не завжди незміщені

Властивості оцінок максимальної правдоподібності.

Метод максимальної правдоподібності для неперервних випадкових величин.

Нехай Х неперервна випадкова величина, яка в результаті n незалежних дослідів приймає значення 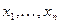. Припускається, що вид щільності закону розподілу відома, але невідомий параметр 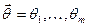який входить до нього, тобто .

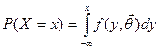Функцією правдоподібності для неперервної випадкової величини Х називають функцію .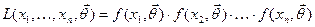

Схема використання методу найбільшої правдоподібності для неперервних випадкових величин така ж сама як і для дискретних.

Для забезпечення «гарних властивостей» оцінок максимальної правдоподібності необхідно виконання деяких спеціальних умов, які називаються умовами регулярності, які накладаються на щільності (у неперервному випадку), або на ймовірності (у дискретному випадку).

Для щільності введемо скорочене позначення .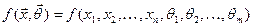

Умови регулярності:

1. Щільність розподілу набору 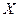така, що область, де 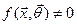для всіх 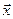, не залежить від параметрів ;

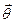2. Вираз можна два рази диференціювати, а вираз можна один раз диференціювати по параметрам.

3. 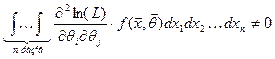при

У випадку коли щільність залежить тільки від одного параметра, тобто умова 3) спрощується і має вигляд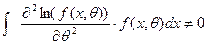

Величина 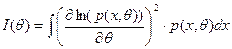називається інформацією(по Фішеру) про невідомий параметр, що міститься в одному незалежному спостереженні.

Дата добавления: 2013-12-13