ЛЕКЦИЯ 1. Трудно переоценить роль Мирового океана в жизни человечества

Трудно переоценить роль Мирового океана в жизни человечества. Однако, можно выделить два важных фактора, без наличия которых само существование человечества было бы невозможным. Во-первых, океан – это огромный резервуар органической жизни и, во-вторых, его наличие играет решающую роль в образовании климата на Земле. Оба эти фактора определяются главным образом подвижностью океанических вод. Без интенсивных горизонтальных и вертикальных перемещений водных масс ресурсы биогенных элементов в верхней фотосинтезирующей зоне океана быстро исчерпаются и океан превратится в безжизненную пустыню. Без горизонтальных движений огромных масс воды немыслима и функция океана как своеобразной «системы центрального отопления» планеты, а без интенсивного вертикального теплообмена теплоемкость этой системы будет ничтожно мала.

Движения вод океана вызываются разнообразными причинами и характеризуются широким спектром пространственных и временных масштабов. Существуют устойчивые глобальные циркуляционные системы, приливные течения, волновые движения различного происхождения, движения вод, вызываемые локальными ветрами и, наконец, разного рода вихревые образования с различной «продолжительностью жизни». Сложная кинематическая структура океана объясняется, во-первых, большим многообразием сил, действующих на океан, и, во-вторых, гидродинамической неустойчивостью движений в океане. Такая неустойчивость приводит к особому типу движения, которое и называется турбулентным. При турбулентном движении поток жидкости характеризуется наложением друг на друга хаотически перемещающихся водных масс (объемов), двигающихся по случайным, меняющим свою форму траекториям. Результатом этих перемещений будут пульсации (или флуктуации) всех термодинамических и гидродинамических характеристик жидкости (т.е. скорости, давления, температуры, концентрации примесей, скорости звука и т.д.). Такие изменения характеристик движущейся жидкости и образуют основу явления турбулентности. Другим типом движения жидкости является ламинарное движение (от латинского слова lamina – слой). В случае ламинарного движения траектории всех частиц параллельны между собой, они движутся по плавным, строго определенным линиям.

Изучение турбулентного режима движения жидкости мы начнем с рассмотрения невозмущенного ламинарного режима для того, чтобы выяснить, при каких условиях происходит разрушение ламинарного течения и возникновение вихревого, неупорядоченного, турбулентного движения жидкости. А для изучения ламинарного движения мы сперва рассмотрим понятие молекулярной вязкости жидкости.

Для уяснения сущности вязкости рассмотрим течение между двумя близко расположенными плоскопараллельными пластинками. Движение возбуждается перемещением одной из пластинок, например, верхней, с постоянной скоростью u₀ относительно неподвижной нижней пластинки. Расстояние между пластинками равно h.

Из опытов известно, что частицы, непосредственно прилегающие к твердой поверхности, как бы при-липают к ней. Таким образом, частицы, прилегающие к нижней пластинке, будут неподвижны, а частицы, непосредственно прилегающие к верхней пластинке, будут двигаться со скоростью u₀. Из опыта также известно, что в условиях постоянства давления в жидкости, между пластинками имеет место линейное распределение скоростей течения, т.е.

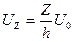(1)

Подобное движение может существовать только в том случае, если к поверхностным частицам жидкости со стороны движущейся пластинки приложена касательная сила. Таким образом, мы воздействуем на поверхностные частицы касательной силой, направленной в сторону движения пластинки и уравновешенной силой внутреннего трения в жидкости. Эта сила, отнесенная к единице площади пластинки, представляет касательное напряжение. Оно пропорционально скорости верхней пластинки (U₀) и обратно пропорционально расстоянию между пластинками (h), т.е. пропорционально отношению U₀/h. Рассмотрим два слоя жидкости на расстоянии Δz друг от друга. Тогда касательное напряжение, оказываемое слоем, движущимся со скоростью U+ΔU на слой, движущийся со скоростью U при условии, что расстояние между слоями равно Δz, пропорционально dU/dz. Обозначая касательное напряжение буквой τ, мы в общем случае можем написать

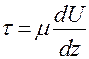(2)

где μ – множитель пропорциональности между τ и dU/dz, зависящий от физической природы жидкости. Этот множитель называется коэффициентом вязкости жидкости. Формула (2) выражает закон трения Ньютона.

Размерность коэффициента вязкости легко получить из формулы (2). Размерность касательного напряжения τ (силы, приложенной к единице площади) есть МL^-1T^-2, а размерность градиента скорости Т^-1. Следовательно,

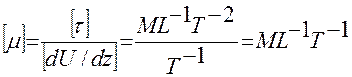
Вязкость морской воды есть функция температуры, солености и давления, причем более всего она зависит от температуры, а менее всего – от давления. Это характеристика, которая известна очень точно. Ее значение, например, для морской воды с температурой 20˚ и соленостью 35%о равно 10.8·10^-3г/(см·сек). С ростом температуры вязкость уменьшается, а с ростом солености – растет.

Так как существование вязкости приводит к замедлению перемещения одних слоев относительно других, следовательно, имеет место действие внутреннего трения в жидкости. Поэтому коэффициент вязкости μ называют также коэффициентом внутреннего трения. При изучении течений, где рассматриваются силы, нормированные на плотность, вводится понятие кинематической вязкости, представляющее отношение вязкости к плотности воды.

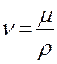(3)

Размерность кинематической вязкости [ν]=L²T^-1.

Составим математическое выражение для силы трения, действующей на некоторый объем жидкости. Для этого рассмотрим в потоке с вертикальным градиентом скорости некоторый объем жидкости высотой Δz и площадью основания, равной единице. Течение направлено по оси х и параллельно одной из граней нашего объема.

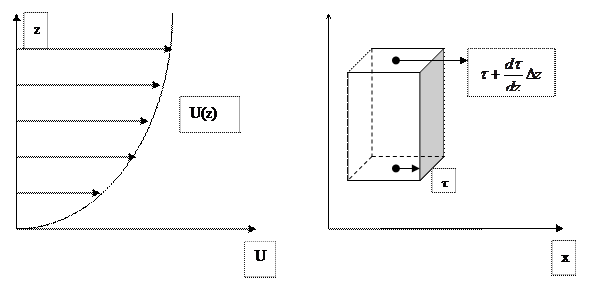
Касательные напряжения, приложенные к верхней и нижней граням выделенного объема, создают силу сдвига, равнодействующая которой, направленная по оси х, равна разности этих напряжений. А сила трения, уравновешивающая равнодействующую силу сдвига, отнесенная к единице объема, равна:

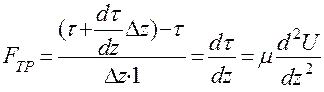(4)

Проявление сил трения происходит вследствие молекулярного перемешивания, т.е. проникновения отдельных молекул из одного элементарного слоя в другой. Если нет причин, поддерживающих разность скоростей в этих слоях, то происходит их постепенное выравнивание вследствие молекулярного перемешивания. Таким образом, действие сил трения есть ни что иное, как перенос количества движения молекулярным перемешиванием.

Течения, в которых закон трения Ньютона проявляется в чистом виде, т.е. в виде проникновения молекул из слоя в слой, и будет называться ламинарным. В нем траектории всех частиц параллельны между собой. В частности, если это движение между двумя параллельными пластинками, то жидкость можно представить в виде бесконечно тонких, наложенных друг на друга слоев, в каждом из которых частицы движутся с одной и той же скоростью.

Ламинарные течения в сплошной среде имеют очень ограниченное распространение в природе. При определенных условиях сложная структура ламинарного течения разрушается, и течение становится турбулентным. Вопрос существования ламинарных течений, а также их разрушения и перехода в турбулентные течения тесно связаны с вопросом о механическом подобии течений.

При каких условиях возможно существование геометрически-подобных течений жидкости, т.е. течений, обладающих геометрически-подобными линиями тока? Очевидно, при том условии, что в подобно расположенных точках силы, действующие на жидкость, находятся в одинаковом соотношении друг к другу, т.е. в жидкости также должно соблюдаться механическое подобие.

Рассмотрим простой случай движения жидкости, когда на частицы действуют только силы инерции и силы внутреннего трения. При этом не будем рассматривать, во-первых, силу тяжести, так как она уравновешивается гидростатическим давлением и, во-вторых, упругие силы, так как будем считать жидкость несжимаемой.

Для установившегося движения, направленного по оси Х, сила инерции, отнесенная к единице объема, равна:

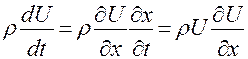(5)

Сила трения, отнесенная к единице объема, равна μ∂²U/∂z². Согласно закону механического подобия, требующего равенства отношений сил в подобно расположенных точках, имеем:

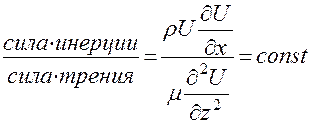(6)

В составленное выражение входят четыре величины, определяющие характер движения: плотность, вязкость, скорость и некоторое линейное расстояние (будем считать, что вертикальные и горизонтальные расстояния – величины одного порядка). Обозначим U – характерная скорость потока, L – характерный линейный размер. Тогда для производных можно записать:

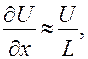
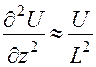
И выражение (6) можно переписать в виде

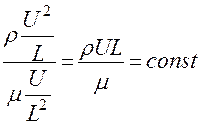(7)

Учитывая, что μ/ρ=ν, можно записать

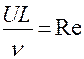(8)

Мы получили критерий механического подобия движения вязкой жидкости, который называется числом Рейнольдса, в честь английского ученого Осборна Рейнольдса, открывшего в 1883 году закон, названный его именем. Это число является важной характеристикой, определяющей относительную роль сил инерции и сил трения в динамике течения. При малых числах Re вязкость оказывает существенное влияние на течение в целом, сглаживая возникающие в нем мелкие неоднородности. При больших числах Рейнольдса силы инерции вызывают перемешивание различных объемов жидкости, движущихся «по инерции» с разными скоростями и способствуют образованию в потоке резких мелкомасштабных неоднородностей, свойственных турбулентным течениям. Поэтому следует ожидать, что течения с достаточно малыми значениями Re будут ламинарными. А с достаточно большими Re – турбулентными.

Представим теперь ламинарное течение, скорость которого постепенно нарастает (либо во времени, либо от одной точки потока к другой, например, при изменении сечения потока). Для сохранения подобия геометрических свойств этого потока необходимо, чтобы увеличение инерционных сил, вызванное ускорением течения, компенсировалось пропорциональным увеличением сил вязкости. Однако, если инерционные силы зависят от скорости потока, то этого нельзя сказать о силах трения, которые зависят прежде всего от физических (молекулярных) свойств жидкости, и в гораздо меньшей степени от скорости потока (сравните ρU∂U/∂x и μ∂²U/∂z²), т.е. силы трения не могут нарастать так же беспрепятственно, как силы инерции. Нарушение механического подобия, т.е. отношения сил инерции и вязкости, влечет за собой нарушение геометрического подобия[1]. Ламинарная структура потока разрушается и он становится турбулентным.

Если вновь обратится к течению между параллельными пластинками, то можно заметить, что введенная в него струйка окрашенной жидкости, которая будет прямолинейной до тех пор, пока течение является ламинарным, с увеличением скорости в определенный момент обрывается, становится беспорядочной, зигзагообразной и постепенно окрашивает всю жидкость. Нарушение ламинарной структуры выражается в том, что помимо основного горизонтального потока появляются дополнительные составляющие скорости, направленные в разные стороны, в том числе и поперек потока. Эти дополнительные составляющие накладываются на основной поток и дополняют медленное молекулярное перемешивание объемным перемешиванием, когда осуществляется взаимное перемещение не только отдельных молекул, но и целых объемов жидкости. Интенсивность объемного перемешивания (турбулентности) зависит уже не от скорости движения молекул и длин их пробегов, а от пульсаций скорости, которые на несколько порядков превышают молекулярные пульсации. Благодаря тому, что количество движения несут уже не отдельные молекулы, а целые объемы жидкости, перемешивание значительно усиливается и профиль скорости выравнивается. Это выравнивание происходит опять же за счет сил трения. Однако эти силы возникают не за счет молекулярного перемешивания, а за счет переноса количества движения целыми объемами жидкости, т.е. турбулентности.

[1] Можно провести аналогию с шариками, катящимися по наклонному лотку. При увеличении скорости шариков, они начинают выскакивать из лотка, уменьшая тем самым массу системы.

Дата добавления: 2013-12-13