Микро-, макро- и метауровни

В зависимости от сложности объекта при его проектировании используют большее или меньшее число уровней абстракции. Объединение уровней, родственных по характеру используемого математического аппарата, приводит к образованию в иерархии функциональных моделей для большинства проектируемых сложных объектов трех укрупненных уровней: микро-, макро- и метауровней.

На микроуровне используют математические модели, описывающие физическое состояние и процессы в сплошных средах. Для моделирования применяют аппарат уравнений математической физики. Примерами таких уравнений служат дифференциальные уравнения в частных производных - уравнения электродинамики, теплопроводности, упругости, газовой динамики. Эти уравнения описывают поля электрического потенциала и температуры в полупроводниковых кристаллах интегральных схем. К типичным фазовым переменным на микроуровне относятся электрические потенциалы, давление, температура, концентрации частиц, плотности токов. Независимыми переменными являются время и пространственные координаты. В качестве операторов 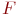и 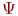в уравнениях (13.2) фигурируют дифференциальные и интегральные операторы. Уравнения (13.2), дополненные краевыми условиями, составляют ММ объектов на микроуровне. Анализ таких моделей сводится к решению краевых задач математической физики.

На макроуровне производится дискретизация пространств с выделением в качестве элементов отдельных деталей, дискретных электрорадиоэлементов, участков полупроводниковых кристаллов. При этом из числа независимых переменных исключают пространственные координаты. Функциональные модели на макроуровне представляют собой системы алгебраических или обыкновенных дифференциальных уравнений. Для их получения и решения используют соответствующие численные методы. В качестве фазовых переменных фигурируют электрические напряжения, токи, силы, скорости, температуры, расходы и т. д. Они характеризуют проявления внешних свойств элементов при их взаимодействии между собой и внешней средой в электронных схемах или механических конструкциях.

На метауровне с помощью дальнейшего абстрагирования от характера физических процессов удается получить приемлемое по сложности описание информационных процессов, протекающих в проектируемых объектах. На метауровне для моделирования аналоговой РЭС широко применяют аппарат анализа систем автоматического управления, а для моделирования цифровой РЭС - математическую логику, теорию конечных автоматов, теорию массового обслуживания. Математические модели на метауровне - системы обыкновенных дифференциальных уравнений, системы логических уравнений, имитационные модели систем массового обслуживания.

Дата добавления: 2013-12-13