Математические модели на макроуровне

Математические модели на микроуровне

Модели на микроуровне используются для исследования напряженного состояния деталей конструкции и для расчетов их на прочность.

Напряженное состояние деталей конструкции в зависимости от геометрии исследуемого узла, вида приложенной нагрузки и свойств материала описывается дифференциальными уравнениями различного вида. Любое из этих уравнений может быть получено из общего квазигармонического уравнения

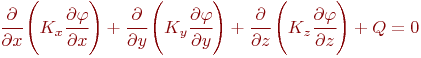
(13.4)

где , , 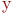- пространственные координаты; 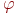- искомая непрерывная функция; , , 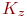- коэффициенты; - внешнее воздействие.

Точное решение краевых задач получают только в частных случаях. Поэтому реализация таких моделей заключается в использовании различных приближенных моделей. Широкое распространение получили модели на основе интегральных уравнений и модели на основе метода сеток. Одним из наиболее популярных методов решения краевых задач в САПР является метод конечных элементов.

Большинство технических подсистем характеризуется фазовыми переменными. Фазовые переменные образуют вектор неизвестных в ММ технической системы. Для каждой физической подсистемы характерны свои законы, однако для простейших элементов форма выражающих их уравнений оказывается одинаковой. Ниже приводится в качестве примера электрическая подсистема.

Электрическая подсистема

Фазовыми переменными электрической подсистемы являются токи I и напряжения U. Запишем уравнения трех типов простейших элементов.

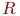1. Уравнение сопротивления (закон Ома) , где - электрическое сопротивление.
2. Уравнение емкости 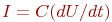, где - электрическая емкость.
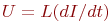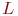3. Уравнение индуктивности , где - электрическая индуктивность.

Дата добавления: 2013-12-13