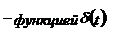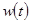Временные характеристики.

К временным характеристикам относятся переходная и весовая характеристики. Их используют при описании линейных систем как стационарных, так и нестационарных.

Переходная функция системы – функция, описывающая изменения выходной величины системы, когда на ее вход подается единичное ступенчатое воздействие при нулевых начальных условиях, или иначе, это функция, описывающая реакцию системы на единичное ступенчатое воздействие при нулевых нормальных условиях (h(t)).

На входе – аналитическое единичное ступенчатое воздействие

1 t h(t) 1 (t)

График переходной функции (зависимость h(t) от времени t) называется переходной характеристикой.

Весовая функция системы - функция, описывающая реакцию системы на единичное импульсное воздействие при нулевых начальных условиях. Она обозначается w(t).

График весовой функции называется весовой или импульсной переходной характеристикой.

Единичный импульс, подаваемый на вход такой системы, описывается дельта-

Она обладает следующими свойствами:

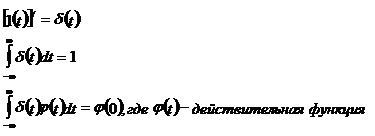
Производные от дельта – функции можно определить из соотношения:

Для линейного дифференциального уравнения:

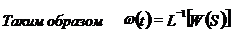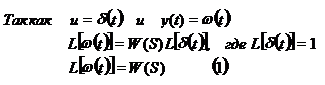
Эту формулу можно использовать для вычисления весовой функции.

Сравнивая (1) и (2) получим:

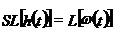
Следовательно:

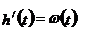
Дата добавления: 2013-12-13