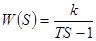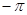КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Элементарные звенья
|
|
|
|
Звено - это математическая модель элемента, соединения элементов или любой части системы.
В общем случае передаточная функция звена может быть описана:
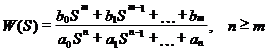
|
то есть дифференциальными уравнениями довольно высокого порядка. Но всегда их можно представить как соединение элементарных звеньев, порядок дифференциальных уравнений которых не выше второго порядка.
Из многочлена числителя и знаменателя выделим элементарные полиномы первого и второго порядка:

|
где di – постоянные действительные коэффициенты.
Поэтому передаточную функцию можно представить как произведение простых множителей и простых дробей.

|

Звенья, передаточные функции которых имеют вид простых множителей, называют элементарными функциями.
Прежде всего, вспомним формулы для модуля и аргумента комплексного числа.
Если есть комплекс число Z, то его можно представить в виде:
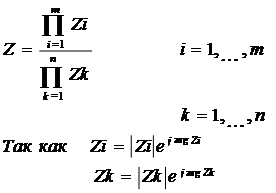
|
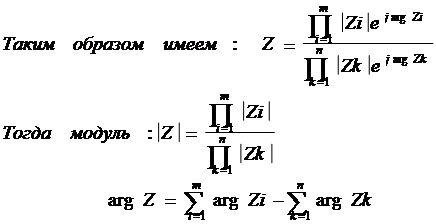
|
Зная модули и аргументы элементарной функций можно получить характеристики любого объекта.
1. Пропорциональное звено - это звено, которое описывается уравнением y(t)=ku(t)
или передаточной функцией W(s)=k.
Частотные и временные функции этого звена:
 
|
АФЧХ  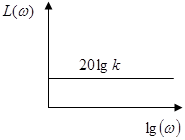 
| ЛАЧХ | Переходная характеристика |
2. Интегрирующее звено – это звено, которое описывается уравнением py=ku
или передаточной функцией W(s)=k/s.
Для этого звена:
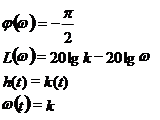 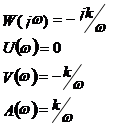
|
| АФЧХ | ЛАЧХ и ЛФЧХ | Переходная характеристика |
3. Дифференцирующее звено описывается уравнением y=kpu или передаточной функцией w(s)=ks.
Частотные и временные функции:
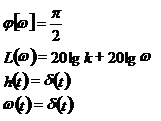 |

|
 АФЧХ АФЧХ 
| ЛАЧХ и ЛФЧХ |
4. Апериодическое звено первого порядка описывается уравнением (Tp+1)y=ku или передаточной функцией W(s)=k/(Ts+1).
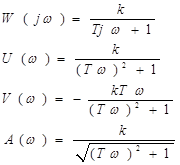
|

|
АФЧХ 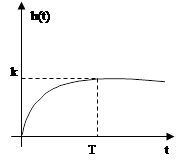 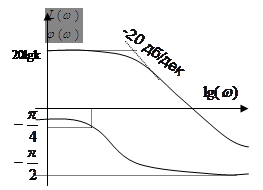 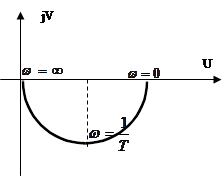
| ЛАЧХ и ФЧХ | Переходная характеристика |
Это звено характеризуется двумя параметрами.
1)Постоянная времени T-время, в течение которого выходная величина, изменяясь с максимальной скоростью, достигает установившегося значения. 2)k- передаточный коэффициент.
5. Неустойчивое апериодическое звено первого порядка.
|
6. Звено чистого запаздывания.

|
Частотные и временные характеристики.
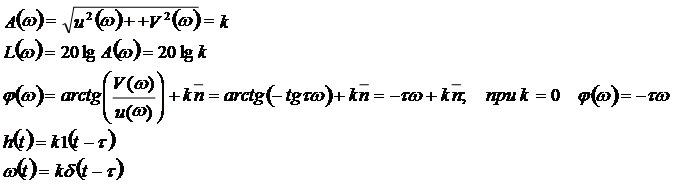
|
Переходная характеристика
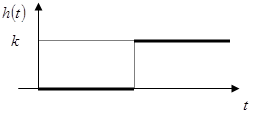
|

Основные элементарные звенья.
1.Пропорциональное w(s)=k
2.Интегральное w(s)=k/s
3.Дифференцирующее w(s)=ks
4.Аппериодическое звено первого порядка w(s)=k/(Ts+1)
5.Колебательное

|
6. Апериодическое звено второго порядка w(s)=k/((T1S+1)(T2 S+1))
7.Консерватианое w(s)=k/(T2S2 +1)
8.Звено чистого запаздывания w(s)=ke- s
|
|
|
|
|
Дата добавления: 2013-12-13; Просмотров: 945; Нарушение авторских прав?; Мы поможем в написании вашей работы!