Теорема Ляпунова

Устойчивость линейных систем автоматического управления.

На любую автоматическую систему всегда действуют различные внешние возмущения, которые могут нарушить ее нормальную работу. Правильно спроектированная система должна устойчиво работать при всех внешних возмущениях.

Понятие устойчивости системы связано со способностью ее возвращаться в состояние равновесия после исчезновения внешних сил, которые вывели ее из этого состояния. Если система неустойчива, то она не возвращается в состояние равновесия, из которого ее вывели.

  Устойчива Неустойчива Безразлична Устойчива в молом, неустойчива в большом

Заданное движение системы при отсутствии возмущений называется невозмущенным движением.

Любое другое движение системы называет возмущенным

Заданное движение называется устойчивым, если после приложения возмущений, которые затем снимают возмущенное движение по истечении некоторого времени войдут в заданную область:

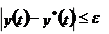
Для исследования систем на устойчивость необходимо получить характеристическое уравнение этой системы. При этом принципиально важны следующие теоремы.

Теорема 1.

Если вещественные части всех корней S_i характеристического уравнения первого приближения отрицательны, то невозмущенное движение асимптотически устойчиво.

Теорема 2.

Если среди корней S_i характеристического уравнения первого приближения имеется хотя бы один корень с положительной вещественной частью, то невозмущенное движение неустойчиво.

Если невозмущенное движение устойчиво и при этом любое возмущенное движение при достаточно малых начальных возмущениях стремится к невозмущенному движению, то есть

где X_i(t) – возмущения.

То невозмущенное движение называют асимптотически устойчивым.

Характеристическое уравнение можно представить в следующем виде:

a_1,1-s а_1,2... а_1,n

а_2,1 а_2,2 - s... а_2,n

D(S) = = 0

а_n,1 а_n,2 ... а_n,n- s

Из него можно найти корни S_i , где i= 1,2,...,n.

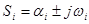В общем виде:

a_i,,w_i - вещественные и мнимые части корней.

Дата добавления: 2013-12-13