
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Математические модели с использованием систем массового обслуживания
|
|
|
|
Эти системы основаны на марковском случайном процессе. Физическая система 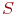 с течением времени меняет свое состояние (переходит из одного состояния в другое) случайным образом. Тогда в системе
с течением времени меняет свое состояние (переходит из одного состояния в другое) случайным образом. Тогда в системе 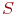 протекает случайный процесс, который называется марковским, если для любого момента времени
протекает случайный процесс, который называется марковским, если для любого момента времени 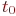 вероятностные характеристики процесса в "будущем" зависят только от его состояния в данный момент времени
вероятностные характеристики процесса в "будущем" зависят только от его состояния в данный момент времени 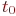 и не зависят от того, когда и как система пришла в это состояние. Вероятностные характеристики в "будущем" можно найти: например, вероятность того, что через некоторое время т система
и не зависят от того, когда и как система пришла в это состояние. Вероятностные характеристики в "будущем" можно найти: например, вероятность того, что через некоторое время т система 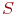 окажется в состоянии
окажется в состоянии 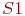 или сохранит состояние
или сохранит состояние 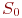 , и т. д.
, и т. д.
Таким образом, в марковском случайном процессе "будущее" зависит от "прошлого" только через "настоящее".
Рассматривая марковские процессы с дискретными состояниями и непрерывным временем, удобно будет представлять, что все переходы системы 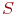 из состояния в состояние происходят под действием каких-то потоков событий (поток вызовов, отказов, восстановлений и т. п.). Если все потоки событий, переводящие систему
из состояния в состояние происходят под действием каких-то потоков событий (поток вызовов, отказов, восстановлений и т. п.). Если все потоки событий, переводящие систему 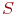 из состояния в состояние, - простейшие, то процесс, протекающий в системе, будет марковским. Это и естественно, так как простейший поток не обладает последействием: в нем "будущее" не зависит от "прошлого".
из состояния в состояние, - простейшие, то процесс, протекающий в системе, будет марковским. Это и естественно, так как простейший поток не обладает последействием: в нем "будущее" не зависит от "прошлого".
Если система S находится в каком-то состоянии 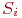 , из которого есть непосредственный переход в другое состояние
, из которого есть непосредственный переход в другое состояние 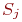 (стрелка, ведущая из
(стрелка, ведущая из 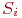 в
в 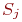 на графе состояний), то это можно представлять так, как будто на систему, пока она находится в состоянии
на графе состояний), то это можно представлять так, как будто на систему, пока она находится в состоянии 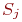 , действует простейший поток событий, приводящий ее по стрелке
, действует простейший поток событий, приводящий ее по стрелке  . Как только появится первое событие этого потока, происходит "перескок" системы из
. Как только появится первое событие этого потока, происходит "перескок" системы из 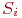 в
в 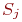 .
.
Для наглядности очень удобно представлять граф состояний. Построим размеченный граф состояний для технического устройства из двух узлов. Состояния системы будут:
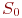 - оба узла исправны;
- оба узла исправны;
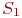 - первый узел ремонтируется, второй исправен;
- первый узел ремонтируется, второй исправен;
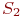 - второй узел ремонтируется, первый исправен;
- второй узел ремонтируется, первый исправен;
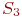 - оба узла ремонтируются.
- оба узла ремонтируются.
Интенсивность потоков событий, переводящих систему из состояния в состояние, вычисляется при условии, что среднее время ремонта узла не зависит от того, ремонтируется ли один узел или оба сразу. Это будет именно так, если ремонтом каждого узла занят отдельный специалист. Найдем все интенсивности потоков событий, переводящих систему из состояния в состояние. Пусть система находится в состоянии 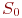 . Какой поток событий переводит ее в состояние
. Какой поток событий переводит ее в состояние 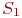 ? Очевидно, поток отказов первого узла. Его интенсивность
? Очевидно, поток отказов первого узла. Его интенсивность 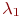 равна единице, деленной на среднее время безотказной работы первого узла. Какой поток событий переводит систему обратно из
равна единице, деленной на среднее время безотказной работы первого узла. Какой поток событий переводит систему обратно из 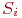 в
в 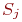 ? Очевидно, поток "окончаний ремонтов" первого узла. Его интенсивность
? Очевидно, поток "окончаний ремонтов" первого узла. Его интенсивность 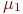 равна единице, деленной на среднее время ремонта первого узла. Аналогично вычисляются интенсивности потоков событий, переводящих систему по всем стрелкам графа рис. 13.2.
равна единице, деленной на среднее время ремонта первого узла. Аналогично вычисляются интенсивности потоков событий, переводящих систему по всем стрелкам графа рис. 13.2.
Имея в своем распоряжении размеченный граф состояний системы, легко построить математическую модель данного процесса.
В самом деле, пусть рассматривается система 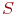 , имеющая
, имеющая 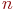 возможных состояний
возможных состояний 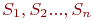 . Назовем вероятностью i-го состояния вероятность
. Назовем вероятностью i-го состояния вероятность 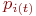 того, что в момент
того, что в момент 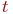 система будет находиться в состоянии
система будет находиться в состоянии 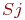 . Очевидно, что для любого момента сумма всех вероятностей состояний равна единице:
. Очевидно, что для любого момента сумма всех вероятностей состояний равна единице:
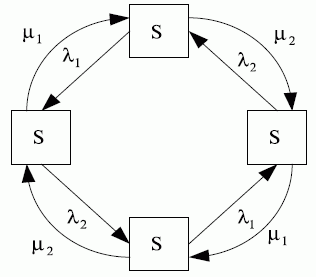
Рис. 13.2. Размеченный граф
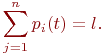
| (13.6) |
Имея в своем распоряжении размеченный граф состояний, можно найти все вероятности состояний 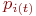 как функции времени. Для этого составляют и решают так называемые уравнения Колмогорова - особый вид дифференциальных уравнений, в которых неизвестными функциями являются вероятности состояний.
как функции времени. Для этого составляют и решают так называемые уравнения Колмогорова - особый вид дифференциальных уравнений, в которых неизвестными функциями являются вероятности состояний.
Рассматривается методика использования основных понятий теории множеств при решении задач конструкторского проектирования.
Содержание
 не является множеством.
Существует два основных способа задания множеств: перечисление и описание.
Первый способ состоит в том, что задаётся и перечисляется полный список элементов, входящих в множество. Например, множество элементов схемы РЭС определяется их списком. Данный способ удобно применять только к ограниченному числу конечных множеств.
Второй способ применяется, когда множество нельзя или затруднительно задать с помощью списка (это может относиться к конечным и бесконечным множествам). В таком случае множества определяются свойствами их элементов.
Множество не является множеством.
Существует два основных способа задания множеств: перечисление и описание.
Первый способ состоит в том, что задаётся и перечисляется полный список элементов, входящих в множество. Например, множество элементов схемы РЭС определяется их списком. Данный способ удобно применять только к ограниченному числу конечных множеств.
Второй способ применяется, когда множество нельзя или затруднительно задать с помощью списка (это может относиться к конечным и бесконечным множествам). В таком случае множества определяются свойствами их элементов.
Множество 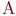 считается заданным, если указано свойство считается заданным, если указано свойство 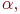 которым обладают все элементы, принадлежащие множеству А, и которым элементы, не принадлежащие множеству которым обладают все элементы, принадлежащие множеству А, и которым элементы, не принадлежащие множеству 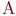 , не обладают.
Если , не обладают.
Если 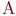 - произвольное множество, а - произвольное множество, а 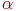 - некоторое свойство, то запись - некоторое свойство, то запись
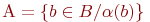 означает множество тех и только тех элементов
означает множество тех и только тех элементов 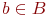 , которые обладают свойством , которые обладают свойством 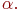 При задании множеств вторым способом необходимо так задавать свойство, характеризующее элементы множества, чтобы оно было общим непротиворечивым для всех его элементов.
Как основное понятие теории, понятие множества не подлежит логическому определению.
Элементы множества могут иметь различную природу. Например, можно говорить о множестве микросхем, входящих в определённую конструкцию РЭС, или о множестве чертежей, входящих в полный комплект конструкторской документации для производства какого-либо изделия.
Множества обозначают заглавными буквами латинского алфавита:
При задании множеств вторым способом необходимо так задавать свойство, характеризующее элементы множества, чтобы оно было общим непротиворечивым для всех его элементов.
Как основное понятие теории, понятие множества не подлежит логическому определению.
Элементы множества могут иметь различную природу. Например, можно говорить о множестве микросхем, входящих в определённую конструкцию РЭС, или о множестве чертежей, входящих в полный комплект конструкторской документации для производства какого-либо изделия.
Множества обозначают заглавными буквами латинского алфавита: 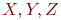 и т.д., а элементы множества - соответствующими строчными буквами того же алфавита: и т.д., а элементы множества - соответствующими строчными буквами того же алфавита: 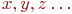 или строчными буквами с индексами: или строчными буквами с индексами: 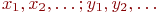 и т.д.
Равенство и т.д.
Равенство  свидетельствует о том, что элементы свидетельствует о том, что элементы 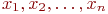 являются элементами множества являются элементами множества  .
Множество можно задавать не только перечислением его элементов, но и с помощью описательного способа, указывающего характерное свойство, которым обладают все элементы этого множества.
Например, если во всём множестве .
Множество можно задавать не только перечислением его элементов, но и с помощью описательного способа, указывающего характерное свойство, которым обладают все элементы этого множества.
Например, если во всём множестве  микросхем электронного блока сложной радиоаппаратуры есть некоторое множество микросхем электронного блока сложной радиоаппаратуры есть некоторое множество 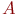 гибридных интегральных схем, то это можно записать так: гибридных интегральных схем, то это можно записать так:
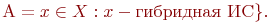 Это читается так: множество
Это читается так: множество 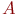 состоит из элементов состоит из элементов 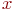 множества множества  , обладающих тем свойством, что , обладающих тем свойством, что 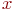 является гибридной интегральной схемой.
Здесь введено новое обозначение является гибридной интегральной схемой.
Здесь введено новое обозначение 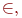 означающее, что объект означающее, что объект 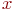 является элементом множества является элементом множества  . Если же некоторый объект . Если же некоторый объект 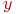 не принадлежит множеству не принадлежит множеству  , то это условие записывают в виде , то это условие записывают в виде 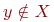 .
В том случае, когда не вызывает сомнения, из какого множества берутся элементы .
В том случае, когда не вызывает сомнения, из какого множества берутся элементы 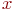 , принадлежность их к множеству , принадлежность их к множеству  можно не указывать.
Например, известно, что множество гибридных интегральных схем входит во множество микросхем того же самого электронного блока, тогда запись будет иметь вид можно не указывать.
Например, известно, что множество гибридных интегральных схем входит во множество микросхем того же самого электронного блока, тогда запись будет иметь вид
 Число элементов множества
Число элементов множества 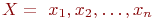 называют мощностью этого множества и обозначают прямыми скобками, например, называют мощностью этого множества и обозначают прямыми скобками, например, 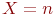 .
Если число элементов множества .
Если число элементов множества  конечно, то такое множество называют конечным.В противном случае множество будет бесконечным.
В теории множеств вводится понятие пустого множества, в котором не содержится ни одного элемента.
Пустое множество обозначают специальным символом конечно, то такое множество называют конечным.В противном случае множество будет бесконечным.
В теории множеств вводится понятие пустого множества, в котором не содержится ни одного элемента.
Пустое множество обозначают специальным символом 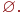 Например, если множество Например, если множество  пусто, то пишут пусто, то пишут 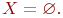 Последовательность из
Последовательность из 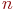 элементов множества называют n - строкой. В отличие от обычного множества, где порядок элементов безразличен, в элементов множества называют n - строкой. В отличие от обычного множества, где порядок элементов безразличен, в 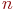 - строке обязательно задаётся их определённая последовательность.
Множество - строке обязательно задаётся их определённая последовательность.
Множество  равно множеству равно множеству 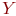 , если оба эти множества состоят из одних и тех же элементов.
Если множество , если оба эти множества состоят из одних и тех же элементов.
Если множество  полностью содержится во множестве полностью содержится во множестве 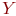 и при этом и при этом 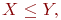 то говорят, что множество то говорят, что множество  является подмножеством множества Y: является подмножеством множества Y:
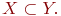 Следовательно, мы рассмотрели два соотношения:
- принадлежность
Следовательно, мы рассмотрели два соотношения:
- принадлежность 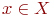 ;
- включение ;
- включение 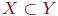 .
Первое определяет связь между множеством и его элементами, а второе - между двумя множествами.
В случае, когда .
Первое определяет связь между множеством и его элементами, а второе - между двумя множествами.
В случае, когда 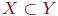 и, одновременно, и, одновременно, 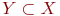 , имеет место равенство , имеет место равенство 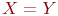 , т.е. множества , т.е. множества  и и 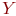 совпадают.
Символическая запись совпадают.
Символическая запись 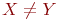 означает, что множество означает, что множество  не совпадает с множеством не совпадает с множеством 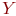 . .
|

|
Лекция: Математические методы описания моделей конструкций РЭС. Элементы теории графов

С использованием введенных в предыдущей лекции элементов теории множеств рассматриваются элементы теории графов при решении задач конструкторского проектирования.
|
|
|
|
|
Дата добавления: 2013-12-13; Просмотров: 291; Нарушение авторских прав?; Мы поможем в написании вашей работы!