Цикломатическое число

Содержание

Основные понятия

Содержание

• 17.1. Основные понятия
• 17. 2. Части графа
• 17. 3. Способы задания графов
• Матрица смежности
• Матрица весовых соотношений
• Матрица инцидентности
• Контрольные вопросы

Изложить основные понятия теории графов, знание которых является обязательным при современном конструкторском проектировании РЭС.

Теорию графов применяют для решения таких задач, как анализ электронных схем, разбиение и размещение электронных элементов, проектирование проводного и печатного монтажа, сетевое планирование и многих других. Это объясняется тем, что использование графов сокращает объём вычислений по сравнению с другими методами и, сохраняя наглядность описания объектов (конструкций), позволяет строить компактные и удобные для реализации на ЭВМ алгоритмы преобразований и оптимизации.

Понятие графа опирается на понятие множества.

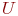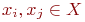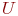Под абстрактным графом или просто графом G(X,U) понимают совокупность непустого множества и изолированного от него подмножества (возможно, пустого), представляющего собой множество всех упорядоченных пар , где . Элементы множеств и называют, соответственно, вершинами и дугами графа. Следовательно, граф - это множество всех вершин 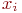, связи между которыми определены множеством рёбер .

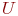Геометрически граф можно представить в виде множества точек в 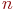-мерном евклидовом пространстве 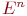и множества простых, направленных самонепересекающихся кривых

соединяющих 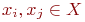, которые находятся в некотором отношении друг к другу.

То, что элемент 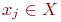находится в отношении 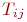к элементу 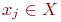, отображается на графе соединением элементов 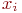и 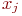линией со стрелкой в направлении от 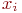к 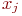. Такие соединения вершин графа с указанием направления называют ориентированными рёбрами или дугами и записывают так:

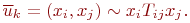
Граф, в котором все вершины соединены дугами, называют ориентированным, направленным или несимметрическим графом.

Аналитически любой ориентированный граф описывается системой алгебраических уравнений, связывающих параметры 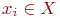, и наоборот, любая система алгебраических уравнений может быть представлена в виде направленного графа.

Пример. Рассмотрим граф, показанный на рис. 17.1.

Рис. 17.1. Ориентированный граф

Этот граф определяет следующую систему уравнений:

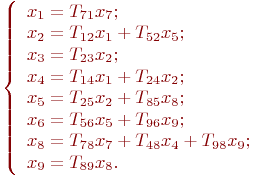
Граф, в котором для любых двух вершин 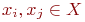справедливо выражение , называют неориентированным, ненаправленным или симметрическим графом.

В таком графе вершины 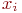и 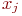соединены ненаправленной кривой, называемой неориентированным ребром или просто ребром графа (рис. 17.2).

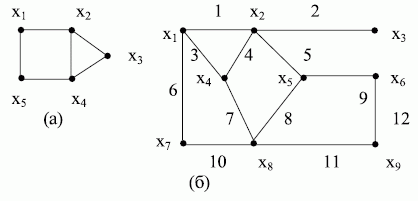
Рис. 17.2. Неориентированные графы

В дальнейшем рассматриваются в основном неориентированные графы, т.к. при решении большинства задач конструкторского проектирования существенным является лишь наличие или отсутствие связей между отдельными элементами конструкции.

При анализе электронных схем, наоборот, пользуются только направленными графами.

На рис. 17.2 неориентированные рёбра обозначены цифрами 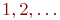.и т.д.

Две вершины 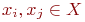считаются смежными, если они определяют ребро (дугу) и, соответственно, два различных ребра (дуги) смежны, если они имеют общую вершину.

Иными словами, вершина 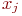смежна 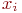, если , где 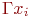- отображение 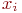на множестве .

В связи с тем, что отображение представляет собой совокупность всех вершин графа , смежных получаем ещё один способ задания графа:

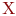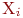Граф задан, если задано непустое множество и отображение множества в 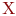. Обозначим его 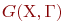. При геометрической реализации такого графа каждую вершину 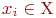соединяют со всеми вершинами .

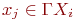Например, для графа 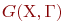(рис. 17.2,б) можно записать:

(.\)

Для графа

(рис. 17.2, а) запись будет следующей:

Вершина 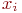инцидента ребру (дуге) если она является началом или концом ребра (дуги). Аналогично утверждение, что ребро (дуга) 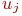инцидентно вершине 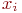, если оно входит или выходит из этой вершины.

Число рёбер (дуг), инцидентных некоторой вершине 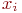, называют локальной степенью вершины и обозначают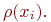

Для графа (рис. 17.2, б) можно записать:

Учитывая, что каждое ребро неориентированного графа инцидентно двум вершинам, получим выражение, связывающее число рёбер графа со степенями вершин

(U()

где 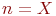- число вершин графа;

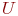- число рёбер графа.

Из этого выражения следует, что число вершин с нечётной степенью в графе чётное, так как при опускании всех вершин 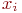с чётными степенями сумма слева остаётся чётной.

Вершину, неинцидентную никакому ребру (дуге), называют изолированной.

Граф, состоящий только из изолированных вершин (), называют нуль - графом и обозначают

При использовании графов для анализа радиоэлектронных устройств в отдельных случаях целесообразно введение связи вершины самой с собой, т.е.

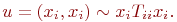
Такую связь называют петлёй.

Если граф имеет петлю при вершине 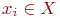, то .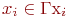

Отсюда следует, что необходимым и достаточным условием отсутствия петель в графе является

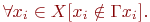
При геометрической реализации графа петля представляется замкнутой дугой, начинающейся и оканчивающейся в одной и той же вершине

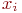
и не проходящей через другие вершины графа. Поскольку концевые точки петли совпадают, то петлю считают неориентированной.

Граф называют конечным,если число его рёбер конечно и бесконечным, если число его рёбер бесконечно.

Граф называют однородным степени t, если степени всех его вершин равны t, т.е.

Лекция: Характеристические числа графов и их применение в конструкторском проектировании РЭС

Рассматриваются некоторые характеристические числа графа, позволяющие в ряде случаев упростить решение задач исследования топологических свойств графа.

• 18. 1. Цикломатическое число
• 18. 2. Хроматическое число
• 18.3. Плоские графы
• Критерии планарности графов
• Разбиение графа на плоские суграфы
• 18.4. Представление конструкции РЭС с помощью графов
• Контрольные вопросы

Изложить основные понятия теории графов, знание которых является обязательным при современном конструкторском проектировании РЭС.

Рассмотрим некоторые характеристические числа графа, позволяющие в ряде случаев упростить решение задач исследования топологических свойств графа. К таким числам, не зависящим от изоморфных преобразований, относятся: цикломатическое 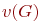и хроматическое числа, числа внутренней 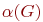и внешней 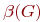устойчивости графа.

При рассмотрении произвольного неориентированного графа без петель с 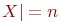и 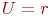, состоящего из " " компонент связности, величину

(18.1)

называют цикломатическим числом графа.

Иногда вводят понятие ранга графа

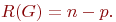
(18.2)

В этом случае цикломатическое число

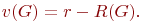
(18.3)

Цикломатическое число графа указывает то наименьшее число рёбер, которое нужно удалить из данного графа, чтобы получить дерево (для связного графа) или лес (для несвязного графа), т.е. добиться отсутствия у графа циклов.

Цикломатическое число всегда неотрицательно.

Основное свойство цикломатического числа формулируется в виде теоремы:

Цикломатическое число мультиграфа равно максимальному числу независимых циклов.

Знание цикломатического числа оказывается полезным при анализе топологии электронных схем, а также для решения целого класса задач конструкторского проектирования РЭС.

Пример. Если рассматривать конструкцию печатной платы, то схему электрических соединений можно интерпретировать графом , где - множество областей контактных площадок, внутри которых проведение проводников запрещено, a 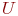- множество трасс.

При этом всё коммутационное пространство разбивается проведёнными соединениями на отдельные, локально замкнутые области

(18.4)

Любые две вершины 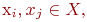находящиеся в различных областях , не могут быть соединены ребром без пересечения рёбер (соединений), ограничивающих област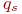и и .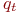

В связи с этим возникает необходимость контроля непопадания смежных вершин в различные изолированные области.

Цикломатическое число 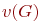позволяет определить число таких локально замкнутых областей и перейти к решению задачи рационального перераспределения рёбер графа .

Дата добавления: 2013-12-13