План лекции. Лекция 1. Функции двух переменных

Лекция 1. Функции двух переменных

1.1. Область определения

1.2. Частные производные

1.3. Градиент и производная по направлению

1.4. Экстремумы

1.5. Нахождение наибольшего и наименьшего значения функции в замкнутой области

1.1. Область определения функции двух переменных

Часто для описания различных процессов недостаточно функций одной переменной. Возникают ситуации, когда интересующее нас значение зависит сразу от нескольких факторов. В таких случаях необходимо рассматривать функцию нескольких

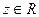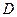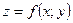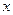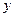Для простоты будем рассматривать функции двух переменных как частный случай функции нескольких переменных. Итак, соответствие , которое каждой паре чисел сопоставляет одно и только одно число , называется функцией двух переменных, определённой на множестве со значениями в , и записывается в виде . При этом и называется независимыми переменными (аргументами), а 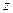- зависимой переменной (функцией).

Множество 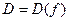называется областью определения функции. Примером функции двух переменных может служить площадь прямоугольника со сторонами, длины которых равны 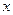и 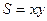. Областью определения этой функции является множество .

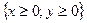Значение функции 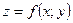в точке обозначается или .

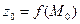Функция 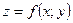называется непрерывной в точке , если она:

- определена в этой точке и некоторой её окрестности,

- имеет предел ,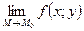

- этот предел равен значению функции 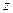в точке , т.е.

или .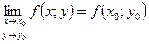

Функция, непрерывная в каждой точке некоторой области, называется непрерывной в этой области. Точки, в которых непрерывность нарушается (не выполняется хотя бы одно из некоторых условий непрерывности функции в точке), называется точками разрыва этой функции. Точки разрыва 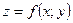могут образовывать целые линии разрыва.

Так, к примеру, функция 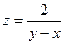имеет линию разрыва 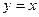, где знаменатель функции обращается в нуль.

Как и в случае функции одной переменной, арифметические операции над непрерывными функциями и построение сложной функции из непрерывных функций приводит к непрерывным функциям.

Если функция 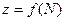непрерывна в ограниченной замкнутой области, то она в этой области:

- ограничена, т.е. существует такое число 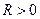, что для всех точек 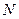в этой области выполняется неравенство ;

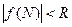- имеет точки, в которых принимает наименьшее значение и наибольшее значения;

- принимает хотя бы в одной точке области численное значение, заключенное между и .

1.2. Частные производные

Частные производные первого порядка

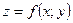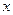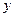Пусть задана функция . Так как и - независимые переменные, то одна из них может меняться, а другая сохранять своё значение. Дадим независимой переменной 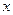приращение 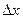, сохраняя значение 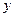неизменным.

Тогда 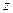получит приращение, которое называется частным приращением 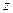по 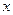и обозначается .

Получаем –

.

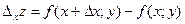Аналогично получается частое приращение 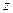по :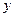

.

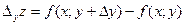Полное приращение функции 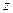определяется равенством:

.

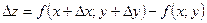Если существует предел:

,

то он называется частной производной функции 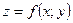в точке 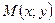по переменной 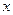и обозначается одним из символов:

, , , .

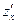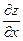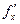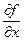Аналогично определяется и обозначается производная от 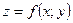по переменной :

.

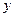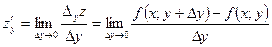Таким образом, частная производная функции нескольких (двух, трёх и дольше) переменных определяется как производная функции одной их этих переменных при условии постоянства значений остальных независимых переменных. Поэтому частные производные функции 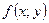находят по формулам и правилам вычисления производных функции одной переменной (при этом соответственно 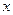и 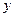считается постоянной величиной).

Пример1. Найти частные производные функции .

При вычислении 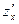рассматриваем переменную y как константу.

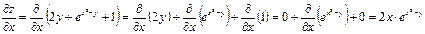
Аналогично вычисляется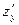

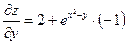
Дифференцируемость и полный дифференциал функции

Пусть функция 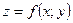определена в некоторой окрестности точки 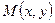. Составим полное приращение функции в точке :

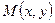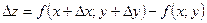
Функция 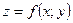называется дифференцируемой в точке 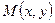, если полное приращение в этой точке можно представить в виде

,

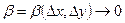где и при .

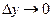Сумма первый двух слагаемых в равенстве представляют собой главную часть приращения функции.

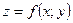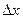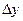Главная часть приращении функции , линейная относительно и , называется полным дифференциалом этой функции и обозначается символом

.

Для независимых переменных 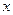и 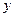полагают, что и , поэтому равенство можно переписать в виде

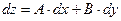
Необходимое условие дифференцируемости. Если функция 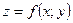, дифференцируема в точке 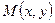, то она непрерывна в этой точке, имеет в ней частные производные 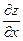и , причём , .

Равенство можно записать в следующем виде

,

где 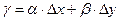при .

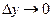Отметим, что обратное утверждение не верно, т.е. из непрерывности функции или существования частных производных не следует дифференцируемость функции.

Так непрерывная функция 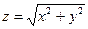не дифференцируема в точке .

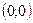Как следствие теоремы получаем формулу для вычисления полного дифференциала. Формула 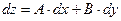, принимает вид:

.

Достаточное условие дифференцируемости. Если функция 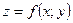имеет непрерывные частные производные в точке 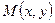, то она дифференцируема в этой точке и её полный дифференциал выражается формулой .

Частные производные высших порядков

Частные производные 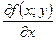и называются частными производными первого порядка. Их можно рассматривать как функцию от . Эти функции могут иметь частные производные, которые называются частными производными второго порядка.

Они определяются следующим образом:

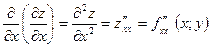
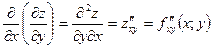
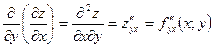
Аналогично определяются частные производные 3-го, 4-го и т.п. порядков. Так,

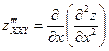
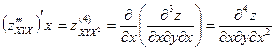
Частная производная второго или более высокого порядка, связанная различными переменными, называется смешанной производной.

Пример 2. Найти частные производные второго порядка функции .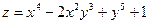

Так как

и , то

;

;

;

.

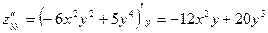Таким образом получаем, что .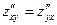

Этот результат не случаен. Имеет место теорема:

Если частные производные высшего порядка непрерывны, то смешанные производные одного порядка, отличающиеся лишь порядком дифференцирования, равны между собой.

В частности, для : .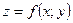

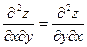1.3. Градиент и производная по направлению

Градиентом функции 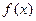, вычисленным в точке (х_о, y_o) называется вектор, компонентами которого являются значения частных производных в этой точке

Если частные производные существуют во всех точках области, то градиент функции, вычисленный в произвольной переменной точке (х, y), представляет собой вектор-функцию .

В некоторых точках (х_о, y_o) градиент может оказаться нулевым вектором, т. е. значения частных производных в точке (х_о, y_o) будут равны 0:

; .

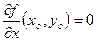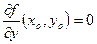Такие точки называются стационарными точками функции .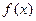

Пример 3. Рассмотрим функцию 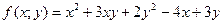заданную на всей числовой плоскости. Найдём частные производные:

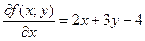
получаем, что

Стационарные точки находятся из системы уравнений

Решая эту систему, находим единственное решение: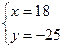

Таким образом, 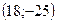- единственная стационарная точка этой функции.

Пусть на плоскости задан некоторый вектор l(l_x, l_y), . Нормируем его, т. е. разделим координаты вектора на его модуль: 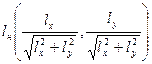. Модуль нормированного вектора равен 1.

Производной функции f(x,y) по направлению l в точке (х_о, y_o) называется предел отношения приращения функции к приращению ее аргументов, при условии, что приращение аргументов происходит по направлению вектора l. Величина этой производной характеризует скорость изменения функции в заданном направлении.

Производная по направлению равна скалярному произведению градиента функции и нормированного вектора направления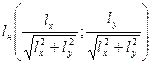

.

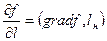Пример 4. Найти производную функции f(x,y) = 3x² + 2xy –y² по направлению l (-3; 4) в точке А(2; 1).

Находим градиент функции в точке: ; ; ;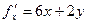

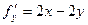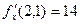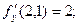
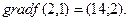
Нормируем вектор направления:

; .

Находим производную по направлению:

.

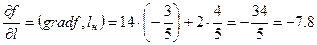Значит, в данной точке в данном направлении функция убывает со скоростью 7.8.

1.4. Экстремум функции двух переменных

Понятие максимума, минимума, экстремума функции двух переменных аналогичны соответствующим понятиям функции одной независимой переменной.

Пусть функция определена в некоторой области 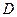, точка . Точка называется точкой максимума функции , если существует такая окрестность точки , что для каждой точки 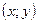, отличной от , из этой окрестности выполняется неравенство .

Аналогично определяется точка минимума функции: для всех точек 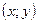, отличных от выполняется неравенство: .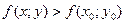

На рисунке (1.1) 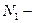точка максимума, а 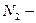точка минимума функции .

Максимум и минимум функции называют её экстремумом.

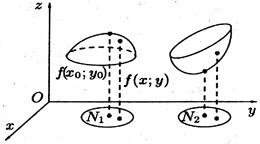
Рис. 1.1

Отметим, что, в силу определения, точка экстремума функции лежит внутри области определения функции; максимум и минимум имеют локальный (местный) характер: значение функции в точке сравнительно с её значениями в точках, достаточно близких к . В области 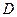функция может иметь несколько экстремумов или не иметь ни одного.

Необходимое условие экстремума. Если в точке 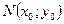дифференцируемая функция имеет экстремум, то её частные производные в этой точке равны нулю: , .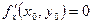

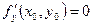Точка, в которой частные производные первого порядка функции равны нулю 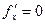, , 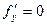называется стационарной точкой функции .

Стационарные точки и точки, в которых хотя бы одна частная производная не существует, называется критическими точками. В критических точках функция может иметь экстремум, а может и не иметь.

Для нахождения экстремумов функции в данной области необходимо каждую критическую точку функции подвергнуть дополнительному исследованию.

Достаточное условие экстремума. Пусть в стационарной точке и некоторой её окрестности функция имеет непрерывные частные производные до второго порядка включительно. Вычислим в точке значения , , 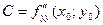. Обозначим

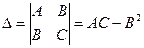
Тогда:

- если , то функция в точке имеет экстремум: максимум, если 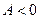; минимум, если ;

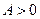- если , то функция в точке экстремума не имеет;

- в случае 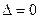экстремум в точке может быть, может и не быть; здесь необходимы дополнительные исследования;

Пример 5. Найти экстремум функции .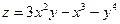

Найдем частные производные: , .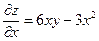

Найдём стационарные точки, приравнивая частные производные к нулю. Получим систему уравнений:

.

Отсюда получаем точк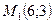и и .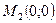

Находим частные производные второго порядка данной функции:

, , .

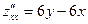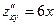В точке 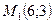имеем: , , 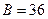, отсюда находим определитель: , т.е. .

Так как 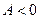, то в точке функция имеет локальный максимум:

.

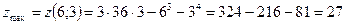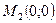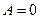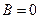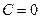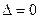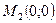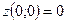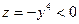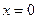В точке : , , а значит . Проведём дополнительное исследование. Значение функции в точке равно нулю: . Так как при и , а также 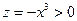при , 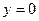. Значит, в окрестности точки 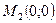функция принимает как отрицательные, так и положительные значения. Следовательно, в точке 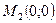функция экстремума не имеет.

1.5. Наибольшее и наименьшее значение функции в замкнутой области

Пусть функция определена и непрерывна в ограниченной замкнутой области D. Согласно теоремам о непрерывной функции, она достигает в некоторой точке этой области своего наибольшего и наименьшего значения.

Если функция дифференцируема в области D, то алгоритм нахождения ее наибольшего и наименьшего значения в этой области заключается в следующем:

1. Найти все критические точки функции, принадлежащие D, и вычислить значения функции в них.

2. Найти наибольшее и наименьшее значение функции на границе области D (это сводится к задаче нахождения максимума и минимума функции одной переменной на отрезке).

3. Среди найденных значений выбрать наибольшее и наименьшее.

Дата добавления: 2013-12-13