Первообразная функция. Определение и свойства

Вступление

Лекция №10

Тема: «Неопределенный интеграл»

1. Первообразная функция. Определение и свойства. 2. Неопределенный интеграл. Определение. Свойства: интеграл от дифференциала, производной; производная и дифференциал от неопределенного интеграла. 3. Таблица интегралов. Вывод двух, трех формул таблицы. Связь с таблицей производных. 4. Непосредственное интегрирование. Интегрирование суммы. Внесение под знак дифференциала. Примеры.    

Одной из основных задач дифференциального исчисления является отыскание производной заданной функции. С помощью операции дифференцирования мы находили, например, мгновенную скорость движущейся точки, зная закон ее движения, находили угловой коэффициент касательной к кривой, представляющий собой график некоторой функции в любой ее точке. Но часто возникает обратная задача - найти закон движения точки, зная ее мгновенную скорость в каждый момент времени (например, самопишущий прибор записывает все показания спидометра, и надо по этим показателям определить положение автомобиля в каждый момент времени). Кроме того, различные вопросы математики и техники приводят к решению обратной задачи дифференцирования - восстановлению функции по заданной производной или дифференциалу. Т.е. решение этих задач сводится к обратной операции интегрирования.

В элементарной математике при решении задач о вычислении и 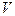тел приходится выполнять громоздкие преобразования, когда используя интегральные исчисления эти задачи решаются очень просто.

Раздел математики, изучающий интегрирование называется интегральным исчислением.

Итак, мы сказали, что основная задача интегрального исчисления это восстановление функции по известной производной этой функции.

Введем необходимые определения.

О.1.1. Функция 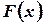называется первообразной для функции 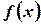на некотором промежутке , если для всех значений из этого промежутка функция 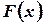непрерывна и выполняется равенство .

Дата добавления: 2013-12-13