Общие аспекты экономики производственного предприятия

Примеры

ТАБЛИЦА ИНТЕГРАЛОВ

Таблица интегралов

Неопределенный интеграл. Определение. Свойства. Примеры.

Примеры.

1) 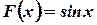является первообразной для функции 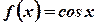, на всей числовой прямой, т.к. для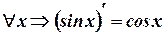

2) 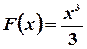- первообразная для 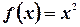, т.е.

Уместен вопрос: для любой ли функции 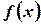существует первообразная ?

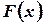Ответ дает теорема 1.

Теорема 1.1. Если функция 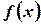непрерывна на промежутке , то для нее на этом промежутке существует первообразная.

Замечание. Если функция 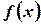имеет точки разрыва, то первообразную для нее будем искать на интервале непрерывности.

Ставится вопрос: а сколько первообразных можно найти для функции .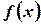

Эта задача решается не однозначно, т.к. например,

.

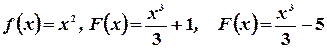Сколько же первообразных? Ответ дает теорема 2.

Теорема 1.2. Если 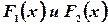первообразные для одной и той же функции 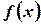, то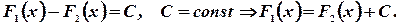

т.е. всякая непрерывная функция имеет бесчисленное множество первообразных, причем две любые из них отличаются на постоянное слагаемое.

Доказательство. Т.к. 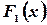есть первообразная для 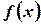, то по определению можно записать .

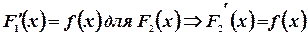Обозначим 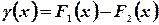и продифференцируем обе части равенства

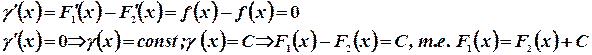
и т.д.

Из теоремы следует, что если 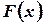первообразная для функции 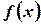, то и 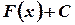тоже является первообразной.

(Свойства: интеграл от дифференциала, производной; производная и дифференциал от неопределенного интеграла)

О.2.1. Неопределенным интегралом функции 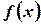называется совокупность всех первообразных .

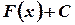Обозначается: .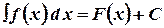

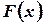- первообразная,

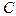- производная постоянная,

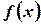- подынтегральная функции,

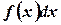- подынтегральное выражение,

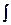- знак интеграла,

х - переменная интегрирования.

Операция нахождения совокупности первообразных, называется интегрированием, а раздел математики, изучающий интегрирование, называется интегральным исчислением.

График функции 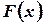называется интегральной кривой функции 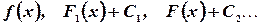- смещены относительно оси ОУ (см. рисунок 1).

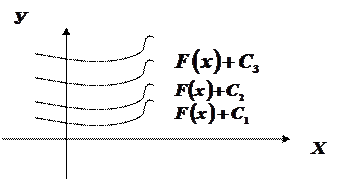Рисунок 1.

Поэтому совокупность всех первообразных (т.е. неопределенный интеграл) составляет семейство интегральных кривых.

Рассмотрим свойства неопределенного интеграла. Т.к. операция интегрирования является обратной для дифференцирования, то свойства неопределенного интеграла легко доказывается действием дифференцирования.

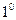. Дифференциал от неопределенного интеграла равен подынтегральному выражению

Доказательство.

Действительно: .

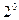. Производная от неопределенного интеграла равна подынтегральной функции, т.е.

.

Доказательство

.

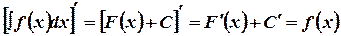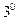. Неопределенный интеграл от дифференциала функции равен сумме этой функции и постоянной

Доказательство

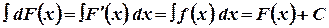ч.т.д.

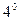. Неопределенный интеграл от производной функции равен самой функции плюс произвольная постоянная, т.е.

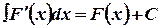
Доказательство

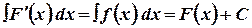
Приведем таблицу основных интегралов. Часть формул следует непосредственно из определения интегрирования, как операции, обратной дифференцированию и таблицы производных.

Справедливость каждой формулы можно проверить путем дифференцирования правой части.

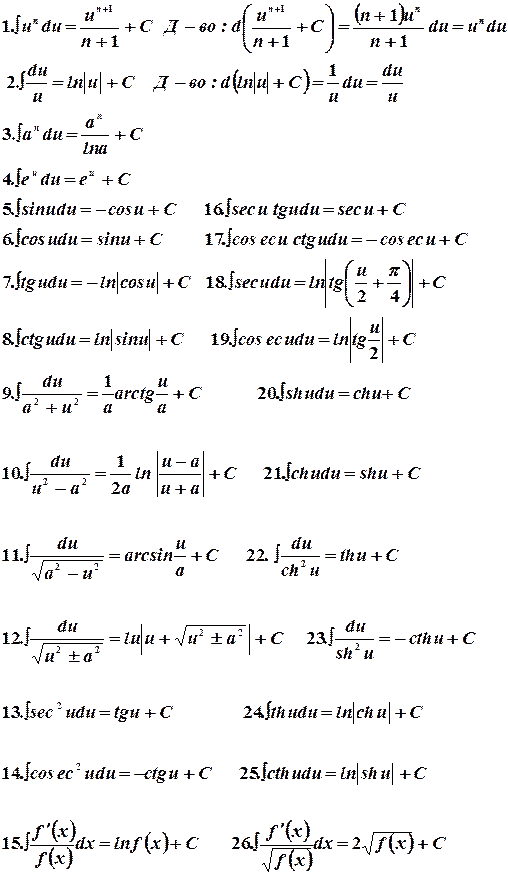
4. Непосредственное интегрирование

Первоначальные навыки по интегрированию связаны с так называемым непосредственным интегрированием, охватывающим применение таблицы интегралов, свойств интегралов и некоторые элементы преобразований, приводящих подынтегральное выражение к виду какого-либо табличного интеграла.

Рассмотрим сначала некоторые правила интегрирования.

4.1 Неопределенный интеграл от алгебраической суммы двух функции

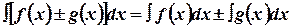
равен алгебраической сумме неопределенных интегралов от этих функций.

Доказательство

Найдем производную от правой и левой части. В силу свойства 2⁰

левое выражение: 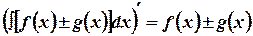(производная от интеграла равна

подынтегральной функции).

правая часть: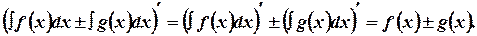

Правые части полученных равенств равны, следовательно, равны и левые части. Ч.т.д.

4.2 Постоянный множитель можно выносить за знак интеграла

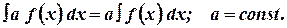
Доказательство

Находим производную левой и правой части.

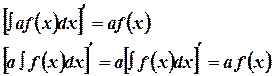и т.д.

4.3 Если 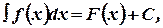то:

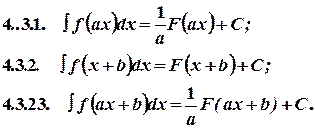
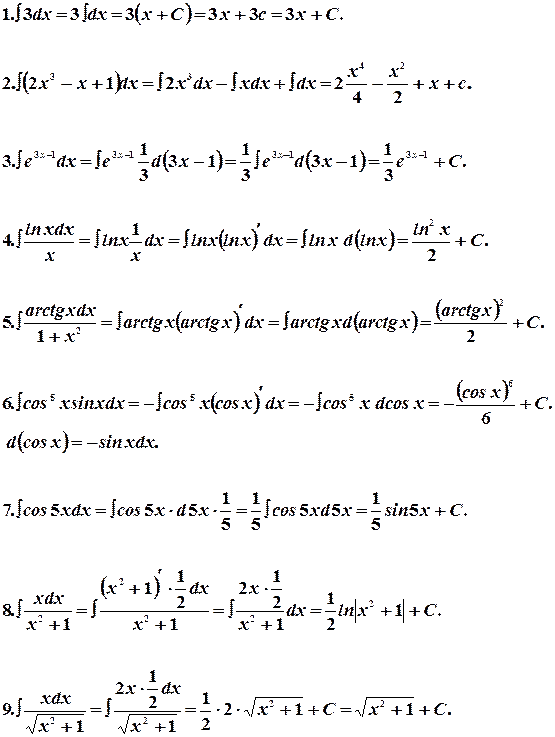
Дата добавления: 2013-12-13