Показатели тесноты связи между двумя количественными признаками

Связь между количественными признаками измеряется через их вариацию. Измерить зависимость (связь) между двумя коррелируемыми величинами – значит определить, насколько вариация результативного признака обусловлена вариацией факторного признака.

В качестве показателей тесноты связи используются (кроме упоминавшегося ранее коэффициента Фехнера – см. §5.2): линейный коэффициент корреляции, коэффициенты корреляции рангов, коэффициент конкордации, а также эмпирическое (см. §5.2) и теоретическое корреляционное отношение (см. §5.6).

Линейный коэффициент корреляции применяется в случае линейной зависимости между двумя количественными признаками x и y, а если форма связи между x и y еще не определена, его рассчитывают с целью получить ответ на вопрос, можно ли считать зависимость линейной. В отличие от К_Ф в линейном коэффициенте корреляции учитываются не только знаки отклонений от средних величин, но и значения самих отклонений, выраженные для сопоставимости в единицах среднего квадратического отклонения t:

и .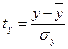

Линейный коэффициент корреляции r представляет собой среднюю величину их произведений нормированных отклонений для x и у:

, (11) или . (12)[7]

Числитель формулы (12), деленный на n, т.е. 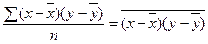, представляет собой среднее произведение отклонений значений двух признаков от их средних, именуемое ковариацией. Поэтому можно сказать, что линейный коэффициент корреляции представляет собой частное от деления ковариации между х и у на произведение их средних квадратических отклонений. Путем несложных математических преобразований можно получить и другие модификации формулы линейного коэффициента корреляции.

Учитывая, что , формулу (12) можно привести к виду

. (13)

Еще одну модификацию можно получить, преобразовав в формуле (12) знаменатель:

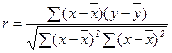. (14)

Иногда линейный коэффициент корреляции удобно рассчитывать по итоговым значениям (суммам) исходных переменных:

(15) или . (16)

Линейный коэффициент корреляции можно рассчитать и по формуле

, (17) где 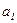– коэффициент регрессии в уравнении связи (см. §5.5).

Линейный коэффициент корреляции может принимать значения от –1 до +1, причем знак определяется в ходе решения. Например, если 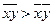, то r по формуле (13) будет положительным, что характеризует прямую зависимость между х и у, в противном случае (r< 0) – обратную связь. Если , то r= 0, что означает отсутствие линейной зависимости между х и у, а при r= 1 – функциональная зависимость между х и у. Следовательно, всякое промежуточное значение r от 0 до 1 характеризует степень приближения корреляционной связи между х и у к функциональной. Таким образом, коэффициент корреляции при линейной зависимости служит как мерой тесноты связи, так и показателем, характеризующим степень приближения корреляционной зависимости между х и у к линейной. Поэтому близость значения r к 0 в одних случаях может означать отсутствие связи между х и у, а в других свидетельствовать о том, что зависимость не линейная.

Пример. Имеются данные по 8 фирмам о часовой оплате труда х и уровне текучести кадров у. Измерить тесноту связи между х и у.

Предположив линейную зависимость между ними, воспользуемся формулой (13), для чего сначала рассчитаем 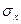и 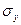(расчет необходимых показателей приведен в таблице):

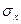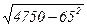===22,9; 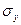===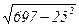8,48.

r =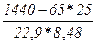=–0,95.

Аналогичный результат получим по формуле (15):

r ==–0,95.

Проверка коэффициента корреляции на значимость (существенность). Интерпретируя значение коэффициента корреляции, следует иметь в виду, что он рассчитан для ограниченного числа наблюдений и подвержен случайным колебаниям, как и сами значения x и y, на основе которых он рассчитан, т.е., как любой выборочный показатель, он содержит случайную ошибку и не всегда однозначно отражает действительно реальную связь между изучаемыми показателями. Для того чтобы оценить существенность (значимость) самого r и, соответственно, реальность измеряемой связи между х и у, необходимо рассчитать среднюю квадратическую ошибку коэффициента корреляции σ_r. Оценка существенности (значимости) r основана на сопоставлении значения r с его средней квадратической ошибкой: . Однако существуют некоторые особенности расчета σ_r в зависимости от числа наблюдений (объема выборки) – n.

1. Если число наблюдений достаточно велико (n>50):

. (18)

Обычно если >3, то r считается значимым (существенным), а связь – реальной. Задавшись определенной вероятностью, можно определить доверительные пределы (границы) r:

,

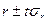где t – коэффициент доверия, рассчитываемый по интегралу Лапласа (см. §3.3).

2. Если число наблюдений небольшое (n<30):

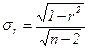, (19)

а значимость r проверяется на основе t- критерия Стьюдента, для чего определяется расчетное значение критерия по формуле (20) и сопоставляется c t_табл.

. (20)

Табличное значение t_табл находится по таблице распределения t -критерия Стьюдента (см. Приложение 2) при уровне значимости α=1-β и числе степеней свободы ν=n–2. Если t_РАСЧ> t_ТАБЛ, то r считается значимым, а связь между х и у – реальной. В противном случае (t_РАСЧ< t_ТАБЛ) считается, что связь между х и у отсутствует, и значение r, отличное от нуля, получено случайно.

Дата добавления: 2013-12-13