Логарифмических и обратных тригонометрических функций

Теорема и формула интегрирования по частям. Правило

Интегрирование по частям.

интегрирования по частям. Интегрирование функций вида ,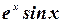

Метод интегрирования по частям основан на использовании формулы дифференцирования произведения двух функций.

Т.2.1. Пусть функции u(x ) и v (x) определены и дифференцируемы на некотором промежутке Х, тогда для всех 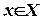справедлива формула

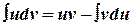(4)

Доказательство

По условию теоремы функции u и v дифференцируемы, следовательно, и непрерывны.

Проинтегрируем обе части этого равенства

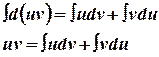
Выразим

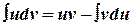ч.т.д.

Правила применения формулы (4):

1. подынтегральное выражение разбить на 2 части, одну из которых обозначить через u, а другую, содержащую дифференциал независимой переменной, через dv;

2. по функции и найдем ее дифференциал du, по dv найдем ;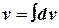

3. результат интегрирования записать по правой части формулы (1).

Пример 4:

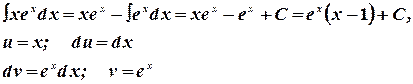
Цель этого метода состоит в том, чтобы подынтегральное выражение vdu стало проще первоначального, поэтому за и надо принимать функцию, которая упрощается при дифференцировании, а за dv ту, по которой легко взять интеграл.

Метод интегрирования по частям применим в случаях интегрирования:

1) логарифмической функции, или ее произведения на какую-либо функцию. При этом за u нужно брать логарифмическую функцию;

2) при интегрировании обратных тригонометрических функций и ее произведения на какую-либо функцию. За u брать обратную тригонометрическую функцию;

3) при интегрировании произведения степенной функции на показательную, степенной на тригонометрическую функцию, за u брать степенную функцию;

4) при интегрировании произведения показательной функции на тригонометрическую. Все равно, что брать за u.

Метод можно повторить несколько раз. Если при повторном применении метода получается исходный интеграл, то надо найти его как неизвестное слагаемое из уравнения.

Пример 5:

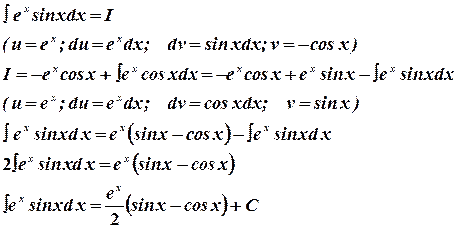
Дата добавления: 2013-12-13