Соотношения неопределенностей

Некоторые свойства волн де Бройля

Рассмотрим свободно движущуюся частицу массой m со скоростью v.

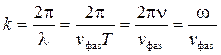
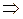
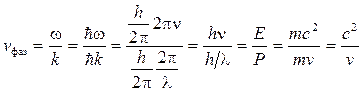, (2)

т.е. фазовая скорость может быть больше скорости света.

Из-за двойственной природы частиц необходимо внести ограничения в применение к объектам микромира законов и понятий классической механики.

В классической механике частица имеет траектори ю, в любой момент времени зафиксирована ее координата и импульс.

Микрочастица из-за волновых свойств существенно отличается от классической частицы. Нельзя говорить о траектории и одновременно точных координатах и импульсе. Понятие «длина волны» лишено физического смысла, т.к. импульс выражается через длину волны (Р = h /l).

В связи с этим немецкий физик Вернер Гейзенберг сформулировал в 1927 г общий принцип, получивший название принципа неопределенности: микрочастица не может иметь одновременно и определенную координату (x) и определенную соответствующую проекцию импульса (Р_x), причем неопределенности этих величин удовлетворяют условию

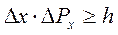
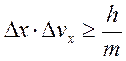. (3)

Смысл (3) состоит в том, что, чем больше масса частицы, тем меньше неопределенность ее координаты и скорости, тем с большей точностью может быть найдена ее траектория.

Пример 1. Пылинка массой m = 10^-12 кг размером l = 10^-6 м, координата определена с точностью 0,01 ее размера (D x = 10^-8м). Неопределенность скорости

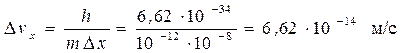
мала и не будет сказываться на скорости движения пылинки. Для описания ее движения можно пользоваться законами классической механики.

Пример 2. Пучок электронов в трубке осциллографа движется со скоростью v = 10⁸ м/c, определяемой с точностью 0,01% (D v_x = 10⁴ м/c). Неопределенность координаты электрона

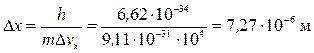
значительно меньше разрешающей способности глаза (0,1 мм = 1×10^-4 м), поэтому движение пучка электронов можно описывать законами классической механики.

Пример 3. Электрон в атоме водорода. Неопределенность координат электрона равна размеру атома (D x» 10^-10 м)

,

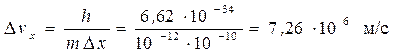неопределенность скорости в несколько раз больше самой скорости (v» 2,3× 10⁶ м/c). Т.о., нельзя пользоваться законами классической механики для описания движения электрона.

Соотношение неопределенностей для энергии и времени: система, имеющая среднее время жизни Dt, не может быть охарактеризована определенным значением энергии; разброс энергии D Е = h /D t возрастает с уменьшением среднего времени жизни:

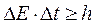(4)

Соотношения неопределенностей - предмет дискуссий. Идеалистическое толкование - соотношение неопределенностей устанавливает границу познаваемости мира. На самом деле это соотношение не ставит предела познанию микромира, а указывает, насколько применимы к нему понятия классической механики.

Идея де Бройля послужила исходным пунктом квантовой механики, созданной в 1926 - 1927 г. трудами В. Гейзенберга, М. Борна, Э. Шредингера, и П.Дирака.

Дата добавления: 2013-12-13