Волновая функция и ее статистический смысл

Принцип дополнительности Н. Бора: всем микрообъектам присущи и волновые, и корпускулярные свойства, однако, они не являются ни волной, ни частицей в классическом понимании. Разные свойства микрообъектов не проявляются одновременно, они дополняют друг друга, только их совокупность характеризует микрообъект полностью. Микрообъекты распространяются как волны, а обмениваются энергией как частицы.

Наличие волновых свойств у микрочастиц сделало невозможным трактовку их как механических частиц. Уравнения движения Ньютона, описывающие движение макрочастиц, непригодны для описания движения микрочастиц. Теория, описывающая движение микрочастиц, должна учитывать все их свойства, корпускулярные и волновые.

Де Бройль, предположивший наличие волновых свойств у частиц, такой теории не создал. Он не нашел уравнения, которое явилось бы для микрочастиц тем, чем является уравнение Ньютона для макроскопических тел. Такое уравнение было найдено Э. Шрёдингером в 1926 г. Так же как и уравнение Ньютона, уравнение Шрёдингера не выводится. Оно постулируется, и его правильность определяется тем, в какой мере его применение подтверждается результатами опыта.

Уравнение Шредингера, определяющее поведение микрочастицы, коренным образом отличается от уравнения Ньютона. Уравнение Ньютона определяет координаты и скорости микрочастиц как функцию времени. Уравнение Шредингера определяет не непосредственно координаты и скорости частиц, а их волновую функцию Y как функцию координат и времени. Уравнение сходно с тем, которое описывает распространение механических волн:

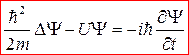, (1)

Y - волновая функция; 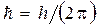- постоянная Планка; m - масса частицы; 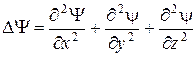- оператор Лапласа; U (x, y, z, t) - потенциальная энергия частицы в силовом поле; 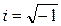- мнимая единица.

Свойства волновой функции

1. Описание микрообъекта имеет статистический (вероятностный) характер: квадрат модуля волновой функции (квадрат модуля амплитуды волн де Бройля) определяет вероятность нахождения частицы в данный момент времени в данном месте.

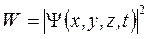. (2)

2. Квадрат амплитудного значения волновой функции определится как произведение Ψ∙Ψ^*, где Ψ^* - комплексно сопряженное значение функции y. Поэтому вероятность нахождения частицы в объеме d V

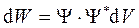.(3)

3. Условие нормировки (объективного существования частицы):

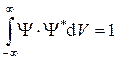. . (4)

4. Ограничительные условия:

· Конечность (вероятность не может быть больше 1);

· Однозначность (вероятность не может быть неоднозначной);

· Непрерывность (вероятность не меняется скачком);

· Удовлетворение принципу суперпозиции

, С_n - произвольные комплексные числа.

Итак, физический смысл функции Y - амплитуда волн де Бройля, а квадратом ее модуля задается интенсивность волн де Бройля.

С помощью волновой функции вычисляются средние значения физических величин, например, среднее расстояние электрона от ядра

.

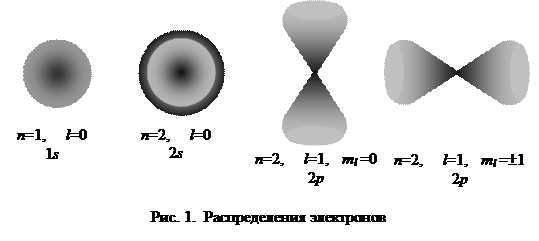
Согласно квантовому представлению для электрона существует лишь электронная плотность вероятности в виде облака, симметрично расположенного около ядра. Электрон не находится на каком - то точно определенном расстоянии от ядра, не существует электронных «орбит», а вместо этого имеется размытое электронное распределение. Можно указать лишь вероятность того, что электрон находится на данном расстоянии от ядра.

5. Уравнение Шрёдингера для стационарных состояний

,

.

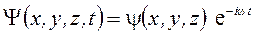
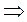
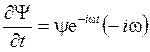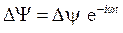
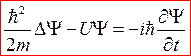
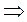
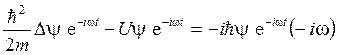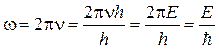
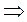
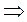
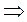
, (5)

Е – полная энергия частицы.

Уравнение в частных производных (5) имеет множество решений, из которых выбирают регулярные решения (имеющие физический смысл). Регулярные решения при определенных

Дата добавления: 2013-12-13