
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лекция 12. Почвенно-экологическая оценка и бонитировка почв
|
|
|
|
Геометрические приложения.
Интегрирование по частям.
Пусть 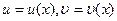 – непрерывно дифференцируемые на сегменте [а,b] функции по формуле Ньютона – Лейбница:
– непрерывно дифференцируемые на сегменте [а,b] функции по формуле Ньютона – Лейбница:


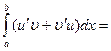
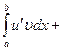
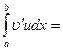

 , откуда
, откуда
- формула интегрирования по частям в


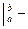
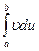 определённом интеграле.
определённом интеграле.
Пример: 
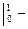
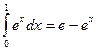
 .
.
5. Приложения определённого интеграла.
· Вычисление площадей плоских фигур в прямоугольной декартово й системе координат.
Пусть 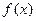 непрерывна на [a,b].
непрерывна на [a,b].
Если  на [a,b], то площадь криволинейной трапеции ограничена линиями
на [a,b], то площадь криволинейной трапеции ограничена линиями 

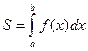
Если 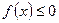 на [a,b],то -
на [a,b],то -  на [a,b], поэтому
на [a,b], поэтому 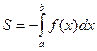 . Тогда объединяя эти два случая, получаем
. Тогда объединяя эти два случая, получаем
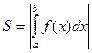
Если линия  пересекает ось ox, то сегмент [a,b] надо разбить на части, в пределах которой
пересекает ось ox, то сегмент [a,b] надо разбить на части, в пределах которой 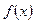 не меняет знака, и вычислить площадь каждой части.
не меняет знака, и вычислить площадь каждой части.
Пример: 1)  и
и 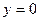

2) 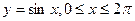 и осью абсцисс (разбить на [0;π]и [π;2π].
и осью абсцисс (разбить на [0;π]и [π;2π].
· Вычисление площади в полярных координатах.
Пусть требуется определить S сектора OAB, ограниченного лучами
(рис. 5) 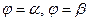 и кривой AB,заданной в полярных координатах уравнением
и кривой AB,заданной в полярных координатах уравнением  , где функция
, где функция  непрерывна на
непрерывна на  .
.
Разобьём отрезок  на
на 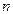 частей точками
частей точками  . Положим
. Положим 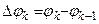 ,
, 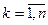 . Наибольшую из этих разностей обозначим
. Наибольшую из этих разностей обозначим  . Разобьём данный сектор на n частей лучами
. Разобьём данный сектор на n частей лучами  . Заменим
. Заменим 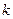 -й сектор круговым сектором радиуса
-й сектор круговым сектором радиуса 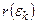 , где
, где 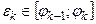 . Тогда сумма
. Тогда сумма 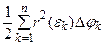 - это приближённая площадь сектора ОАВ. Отсюда
- это приближённая площадь сектора ОАВ. Отсюда 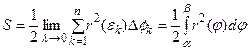 .
.
Пример: Найти площадь плоской фигуры, ограниченной кардиоидой  .
.
Учитывая симметричность кривой, имеем:
 .-
.-
· Вычисление длины дуги.
1) Пусть дуга АВ задана уравнением  ,
,  , где
, где  имеет на
имеет на 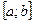 непрерывную производную. Длиной дуги АВ называется предел, к которому стремится длина ломаной линии, вписанной в эту дугу, когда длина наибольшего звена стремится к нулю. Разобьем отрезок
непрерывную производную. Длиной дуги АВ называется предел, к которому стремится длина ломаной линии, вписанной в эту дугу, когда длина наибольшего звена стремится к нулю. Разобьем отрезок
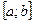 точками
точками  на n частей, положим
на n частей, положим  . Наибольшую из этих разностей обозначим через
. Наибольшую из этих разностей обозначим через  . Поставим точки
. Поставим точки 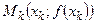 ,
, 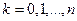 . Обозначим
. Обозначим  – приращение функции на отрезке
– приращение функции на отрезке  . По теореме Пифагора
. По теореме Пифагора  .
.
По формуле Лагранжа 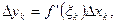 , где
, где 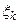 - некоторая промежуточная точка отрезка
- некоторая промежуточная точка отрезка  . Отсюда
. Отсюда 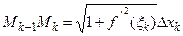 . Следовательно, длина ломаной линии
. Следовательно, длина ломаной линии 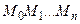 равна
равна  , переходя к пределу при
, переходя к пределу при 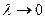 , получим
, получим 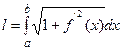 . Дифференциал дуги
. Дифференциал дуги 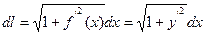
2) Если кривая АВ задана параметрическими уравнениями  , причём функции
, причём функции  и
и  имеют непрерывные производные
имеют непрерывные производные 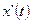 и
и  на
на  , то путём замены переменной
, то путём замены переменной 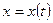 получим
получим 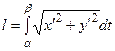 . Формула дифференциала дуги будет
. Формула дифференциала дуги будет 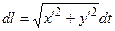
3) Если кривая АВ задана в полярных координатах уравнением  , то, учитывая связь между прямоугольными и полярными координатами, параметрические уравнения этой кривой будут:
, то, учитывая связь между прямоугольными и полярными координатами, параметрические уравнения этой кривой будут:

Поэтому 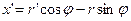
 , тогда получим:
, тогда получим:
 .
.
Формула дифференциала дуги будет 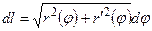
Пример 1. Найти длину дуги линии 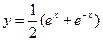 при
при 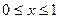
Пример 2. Вычислить длину окружности радиуса R.
В полярных координатах уравнение окружности  при
при  .
.
Тогда 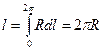 .
.
· Площадь поверхности вращения.
Пусть дуга  задана уравнением
задана уравнением 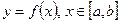 , где
, где 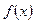 – функция, имеющая на
– функция, имеющая на 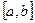 непрерывную производную. Поверхность, образованная вращением
непрерывную производную. Поверхность, образованная вращением 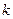 -го звена ломаной
-го звена ломаной  вокруг оси ОХ, есть боковая поверхность усечённого конуса с площадью
вокруг оси ОХ, есть боковая поверхность усечённого конуса с площадью
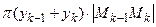 или
или  , где
, где  .
.
Следовательно, площадь поверхности вращения ломанной 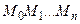 вокруг оси
вокруг оси 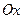 равна
равна 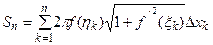 . Площадь поверхности вращения дуги
. Площадь поверхности вращения дуги  вокруг оси
вокруг оси 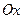 определим
определим
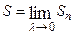 , где
, где  . Заметим, что сумма
. Заметим, что сумма 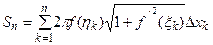 не является интегральной для функции
не является интегральной для функции 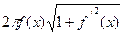 , так как взяты значения функции
, так как взяты значения функции 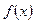 в разных точках отрезка. Но можно доказать, что
в разных точках отрезка. Но можно доказать, что 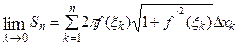 .
.
Поэтому  - формула площади поверхности вращения в прямоугольной декартовой системе координат.
- формула площади поверхности вращения в прямоугольной декартовой системе координат.
Аналогично, учитывая формулы дифференциала дуги, получаем выражения для площади поверхности вращения для функции, заданной параметрическими уравнениями
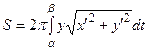
и для функции, заданной в полярных координатах
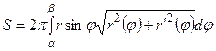
· Вычисление объёма.
Рассмотрим тело, содержащееся между плоскостями 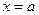 и
и 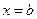 . Пусть для каждого
. Пусть для каждого  из сегмента
из сегмента 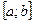 дана площадь сечения этого тела
дана площадь сечения этого тела  , перпендикулярного оси
, перпендикулярного оси 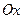 . Разделим сегмент
. Разделим сегмент 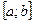 на
на 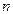 частей и через точки деления проведём плоскости перпендикулярные оси
частей и через точки деления проведём плоскости перпендикулярные оси 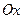 . Эти плоскости разобьют тело на слои. Тогда объём
. Эти плоскости разобьют тело на слои. Тогда объём 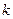 -го слоя, ограниченный плоскостями
-го слоя, ограниченный плоскостями  и
и 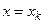 , будет
, будет 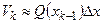 . Образуем сумму
. Образуем сумму  . Тогда
. Тогда  , если функция
, если функция  непрерывна на
непрерывна на 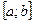 .
.
Таким образом, 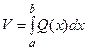 - формула для вычисления объема по площади поперечного сечения.
- формула для вычисления объема по площади поперечного сечения.
В частности, если тело образовано поверхностью вращения линии  вокруг оси
вокруг оси 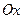 в пределах изменения
в пределах изменения  от
от  до
до 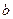 , то
, то  и
и
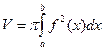 .
.
Пример: Найти объём тела, образованного вращением плоской фигуры, ограниченной линиями  и
и 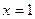 вокруг оси
вокруг оси 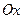 .
.
 .
.
5.2 Физические приложения определённого интеграла.
Статическим моментом материальной точки, находящейся в плоскости XOY, относительно координатной оси Ох (или Оу) называется произведение массы этой точки на её ординату (соответстветственно абсциссу). Статическим моментом системы таких точек  относительно координатной оси называется сумма статических моментов всех точек системы относительно этой оси.
относительно координатной оси называется сумма статических моментов всех точек системы относительно этой оси.
Центром тяжести системы материальных точек с массами 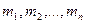 называется точка С, обладающая тем свойством, что если в ней сосредоточить всю массу системы, то её статический момент по отношению к любой оси равен статическому моменту системы точек относительно той же оси.
называется точка С, обладающая тем свойством, что если в ней сосредоточить всю массу системы, то её статический момент по отношению к любой оси равен статическому моменту системы точек относительно той же оси.
Пусть дуга АВ задана уравнением 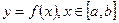 , где
, где 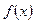 имеет на
имеет на 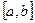 непрерывную производную, и на этой дуге распределено вещество с плотностью
непрерывную производную, и на этой дуге распределено вещество с плотностью 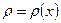 . Тогда масса материальной дуги:
. Тогда масса материальной дуги:
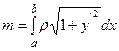 а её статические моменты относительно координатных осей:
а её статические моменты относительно координатных осей: 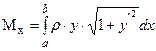 ,
, 
Координаты центра тяжести:
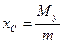 ,
, 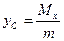
Для плоской фигуры, ограниченной линиями 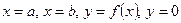 , на которой распределено вещество с плотностью
, на которой распределено вещество с плотностью  масса и статические моменты всей фигуры вычисляется по формулам
масса и статические моменты всей фигуры вычисляется по формулам
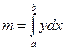 ,
, 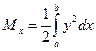 ,
, 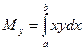 .
.
Координаты центра тяжести как и для дуги: 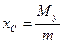 ,
, 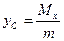 .
.
5.3. Биологические и экологические приложения определённого интеграла.
· Численность популяции.
Число особей в популяции меняется со временем. Если условия существования популяции благоприятны, то рождаемость превышает смертность и общее число особей в популяции растёт со временем. Назовём скоростью роста популяции прирост числа особей в единицу времени. Если известна скорость роста популяции 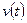 , то мы можем найти прирост численности популяции за промежуток времени от
, то мы можем найти прирост численности популяции за промежуток времени от  до
до 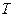 .
.
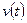 следует, что эта функция является производной от численности популяции
следует, что эта функция является производной от численности популяции 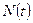 в момент
в момент  , и, следовательно, численность популяции является первообразной для
, и, следовательно, численность популяции является первообразной для 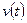 . Поэтому
. Поэтому 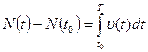 или
или  .
.
Так например, в условиях неограниченных ресурсов питания скорость роста многих популяций экспоненциально, то есть  .
.
Тогда 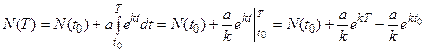
По этой формуле, например, можно вычислить численность популяции микроорганизмов, которые пересаживаем время от времени в новые ёмкости с питательной средой (например, культивируемых плесневых грибков, выделяющих пенициллин).
· Биомасса популяции.
Рассмотрим популяцию, в которой масса особи заметно меняется в течение жизни, и подсчитаем общую биомассу популяции.
Пусть  означает возраст в тех или иных единицах времени,
означает возраст в тех или иных единицах времени,
 – число особей популяции возраста
– число особей популяции возраста  ,
,
 – средняя масса особи возраста
– средняя масса особи возраста  ,
,
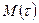 – биомасса всех особей в возрасте от 0 до
– биомасса всех особей в возрасте от 0 до  .
.
Можно показать, что биомасса 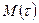 является первообразной для
является первообразной для 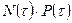 , то есть
, то есть 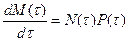 , отсюда
, отсюда  , где
, где 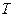 – максимальный возраст особи в данной популяции. Так как
– максимальный возраст особи в данной популяции. Так как 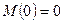 , то
, то 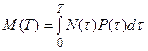 .
.
Существуют и другие примеры возможных приложений определённого интеграла в биологии.
· Средняя длина пролета птиц.
Рассмотрим задачу о вычислении средней длины пролета птиц при прохождении некоторого фиксированного участка. Пусть участком будет круг радиуса  . Будем считать, что
. Будем считать, что  не слишком велико, так что большинство птиц изучаемого вида пересекают этот круг по прямой. Птица может под любым углом в любой точке пересечь окружность. В зависимости от этого длина ее пролета над кругом может быть равной любой величине от 0 до
не слишком велико, так что большинство птиц изучаемого вида пересекают этот круг по прямой. Птица может под любым углом в любой точке пересечь окружность. В зависимости от этого длина ее пролета над кругом может быть равной любой величине от 0 до 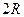 .
.
Так как круг симметричен относительно любого своего диаметра, то ограничимся птицами, которые летят в одном каком-нибудь направлении, параллельном оси 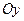 . Тогда средняя длина пролета – это среднее расстояние между дугами
. Тогда средняя длина пролета – это среднее расстояние между дугами 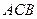 и
и 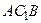 , т.е. среднее значение функции
, т.е. среднее значение функции  , где
, где 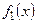 - уравнение верхней дуги окружности, а
- уравнение верхней дуги окружности, а 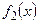 - уравнение нижней дуги окружности. Тогда средняя длина пролета
- уравнение нижней дуги окружности. Тогда средняя длина пролета
 .
.
|
|
|
|
|
Дата добавления: 2013-12-13; Просмотров: 843; Нарушение авторских прав?; Мы поможем в написании вашей работы!