
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Использование симметричной основной системы метода сил
|
|
|
|
Введение
Лекция 13
Особые методы расчёта статически неопределимых рам методом сил.
Расчёт статически неопределимого сооружения на любые воздействия с математической точки зрения сводится к решению системы линейных алгебраических неоднородных уравнений, число неизвестных которой равно степени статической неопределимости сооружения. Решение этой системы уравнений требует большого объёма времени, особенно в расчётах сооружений с высокой степенью статической неопределимости. Сократить время решения системы канонических уравнений, составленной для расчёта заданного сооружения, можно выбирая основную систему метода сил так, чтобы возможно большее число побочных коэффициентов при неизвестных dij приняли нулевое значение. В этом случае система уравнений будет неполной, а в случае, когда все побочные коэффициенты dij равны нулю, она распадается на отдельные уравнения, каждое из которых содержит только одно неизвестное.
Принципиально такого рода задача может быть решена соответствующим выбором основной системы и неизвестных метода сил для любого статически неопределимого сооружения. Наиболее же просто она решается для сооружений, геометрия которых и распределение жесткостей поперечных сечений элементов, обладает хотя бы одной осью симметрии. Расчёт такого рода сооружений целесообразно проводить, используя симметричную основную систему метода сил (см. п. 18.2 и 18.3 настоящей лекции).
Если для расчёта рамы, имеющей вертикальную ось симметрии (рис. 13.1,а) на произвольное воздействие (силовое, температурное или кинематическое) использовать несимметричную основную систему метода сил, показанную на рис. 13.1,б, то этот расчёт сведётся к решению полной системы четырёх алгебраических неоднородных уравнений с четырьмя неизвестными Х1, Х2, Х3, Х4. Эта система уравнений для рассматриваемой задачи примет вид:
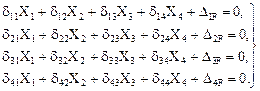 (13.1)
(13.1)
|
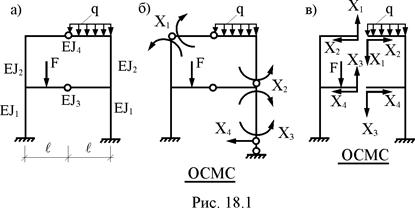
Приняв для расчёта рамы симметричную основную систему (рис. 13.1,в), мы будем иметь дело с обратносимметричными (Х1 и Х3) и симметричными неизвестными (Х2 и Х4). От единичных значений этих неизвестных эпюры внутренних усилий будут обратносимметричными или симметричными. В частности, для рассматриваемой рамы, учитывая только деформации изгиба её элементов, в основной системе будем иметь: эпюры М1 и М3, соответственно, от Х1 = 1 и Х3 = 1 – обратносимметричными, эпюры М2 и М4 от Х2 = 1 и Х4 = 1 –симметричными.
Сопрягая обратносимметричные эпюры изгибающих моментов М1 и М3 с симметричными – М2 и М4, получим:
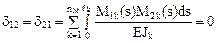 ,
,
 ,
,
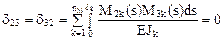 ,
,
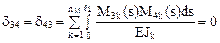 .
.
С учётом нулевых значений вышеперечисленных побочных коэффициентов система канонических уравнений метода сил (13.1) распадётся на две независимых друг от друга системы двух уравнений с двумя неизвестными, причём первая из этих систем уравнений будет содержать только обратносимметричные неизвестные, а вторая – только симметричные.
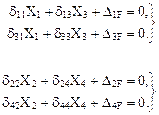
|
|
|
|
|
Дата добавления: 2013-12-13; Просмотров: 471; Нарушение авторских прав?; Мы поможем в написании вашей работы!