
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Группировка неизвестных метода сил
|
|
|
|
|
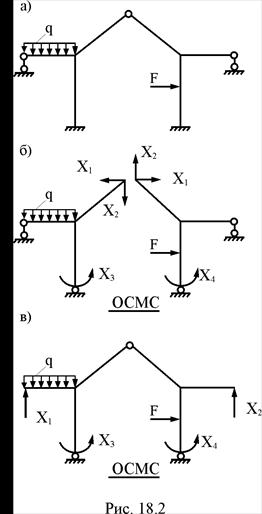 Часто при выборе симметричной основной системы не всегда удаётся получить только симметричные и обратносимметричные неизвестные метода сил. Например, рассмотрим для симметричной рамы (рис. 13.2,а) два варианта симметричной основной системы метода сил. Первый вариант (рис. 18.2,б) содержит симметричное неизвестное Х1, обратносимметричное Х2 и несимметричные неизвестные Х3 и Х4. Во втором варианте (рис. 13.2,в) все неизвестные метода сил Х1, Х2, Х3, Х4 несимметричны. Использование рассматриваемых вариантов симметричных основных систем для расчёта рамы на произвольную нагрузку при указанных наборах неизвестных метода сил не приведёт к разделению одной группы неизвестных метода сил от другой в системе канонических уравнений, так как в единичных состояниях первого варианта основной системы только часть эпюр внутренних усилий будут носить симметричный (от Х1 = 1) или обратносимметричный (Х2 = 1) характер, а во втором варианте основной системы таких эпюр внутренних усилий вообще не будет.
Часто при выборе симметричной основной системы не всегда удаётся получить только симметричные и обратносимметричные неизвестные метода сил. Например, рассмотрим для симметричной рамы (рис. 13.2,а) два варианта симметричной основной системы метода сил. Первый вариант (рис. 18.2,б) содержит симметричное неизвестное Х1, обратносимметричное Х2 и несимметричные неизвестные Х3 и Х4. Во втором варианте (рис. 13.2,в) все неизвестные метода сил Х1, Х2, Х3, Х4 несимметричны. Использование рассматриваемых вариантов симметричных основных систем для расчёта рамы на произвольную нагрузку при указанных наборах неизвестных метода сил не приведёт к разделению одной группы неизвестных метода сил от другой в системе канонических уравнений, так как в единичных состояниях первого варианта основной системы только часть эпюр внутренних усилий будут носить симметричный (от Х1 = 1) или обратносимметричный (Х2 = 1) характер, а во втором варианте основной системы таких эпюр внутренних усилий вообще не будет.
Ситуация изменится, если в качестве неизвестных метода сил использовать симметричные и обратносимметричные групповые неизвестные. Искусственной группировке подлежат неизвестные реакции в симметрично расположенных лишних связях, чаще всего – в двух. В частности, для нашего примера: в первом варианте основной системы (рис. 13.2,б) – это Х3 и Х4, а во втором (рис. 13.2,в) – Х1 и Х2, Х3 и Х4.
 Кинематические условия, на базе которых составляется система канонических уравнений метода сил, естественно, должны быть выполнены. Так, для основной системы, показанной на рис. 13.2,в, неизвестные метода сил подбираются из условий равенства нулю перемещений по направлению Х1, Х2, Х3, Х4 от действия всех неизвестных метода сил и заданной нагрузки, т.е. из условий:
Кинематические условия, на базе которых составляется система канонических уравнений метода сил, естественно, должны быть выполнены. Так, для основной системы, показанной на рис. 13.2,в, неизвестные метода сил подбираются из условий равенства нулю перемещений по направлению Х1, Х2, Х3, Х4 от действия всех неизвестных метода сил и заданной нагрузки, т.е. из условий:
D1 = 0, D2 = 0, D3 = 0, D4 = 0.
Эти условия будут выполнены, если в рассматриваемой основной системе отрицать групповые перемещения, а именно:
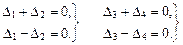
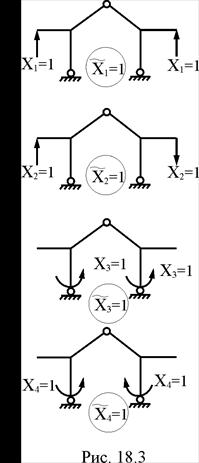
Указанным групповым перемещениям соответствуют групповые неизвестные метода сил  , которые являются симметричными или обратносимметричными. Единичные состояния, соответствующие принятым групповым неизвестным, показаны на рис. 13.3.
, которые являются симметричными или обратносимметричными. Единичные состояния, соответствующие принятым групповым неизвестным, показаны на рис. 13.3.
|
 запишется:
запишется: (13.2)
(13.2)
В системе уравнений (18.2) 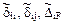 – групповые перемещения в основной системе, соответственно, от единичных групповых неизвестных и заданной нагрузки. Учитывая симметричный характер групповых неизвестных
– групповые перемещения в основной системе, соответственно, от единичных групповых неизвестных и заданной нагрузки. Учитывая симметричный характер групповых неизвестных 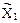 и
и  и обратносимметричный –
и обратносимметричный – 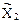 и
и 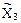 , как и в п. 18.2 настоящей лекции, получим:
, как и в п. 18.2 настоящей лекции, получим:
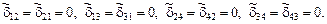
С учётом нулевых значений восьми побочных коэффициентов система уравнений (18.2) распадётся на две системы двух уравнений с двумя неизвестными:
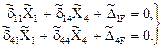
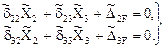
Первая из приведённых систем уравнений содержит только симметричные групповые неизвестные 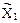 и
и  , а вторая – только обратносимметричные
, а вторая – только обратносимметричные 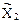 и
и 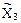 .
.
При построении эпюр внутренних усилий в заданном сооружении различий между обычными и групповыми неизвестными метода сил не делают. Например, эпюру изгибающих моментов в статически неопределимой раме, показанной на рис. 13.2,а, от действия произвольной нагрузки, можно получить, имея эпюры изгибающих моментов  в групповых единичных состояниях и зная численные значения групповых неизвестных
в групповых единичных состояниях и зная численные значения групповых неизвестных  , следующим образом:
, следующим образом:
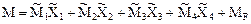 .
.
|
|
|
|
|
Дата добавления: 2013-12-13; Просмотров: 1465; Нарушение авторских прав?; Мы поможем в написании вашей работы!