
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Итерационные методы решения интегральных уравнений в свертках
|
|
|
|
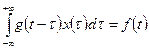 (1)
(1)
Предполагаем, что образ Фурье функции 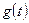 функция
функция  при изменении
при изменении  в интервале
в интервале  обращается в нуль в конечном числе точек. Обоснование итерационных алгоритмов будем проводить в пространстве
обращается в нуль в конечном числе точек. Обоснование итерационных алгоритмов будем проводить в пространстве  .
.
Будем обозначать через 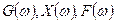 преобразование Фурье функций
преобразование Фурье функций  .
.
Будем говорить, что выполнено условие А, если в плоскости комплексной переменной z множество значений  расположено внутри угла с вершиной в начале координат и с раствором, меньшим
расположено внутри угла с вершиной в начале координат и с раствором, меньшим 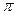 , причем при конечных значениях
, причем при конечных значениях  функция
функция  не равна нулю. Тогда найдется такая константа
не равна нулю. Тогда найдется такая константа  (в общем случае комплексная), что множество значений
(в общем случае комплексная), что множество значений  будет расположено внутри и на окружности с центром в точке
будет расположено внутри и на окружности с центром в точке 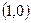 с радиусом, равным 1.
с радиусом, равным 1.
Пусть спектры входного и выходного сигналов расположены в сегменте  и выполнено условие А. Тогда найдется такая константа
и выполнено условие А. Тогда найдется такая константа  , при которой
, при которой  .
.
Рассмотрим итерационный процесс:
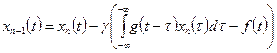 (2)
(2)
Теорема 1. Пусть спектры входного и выходного сигналов расположены в сегменте  и выполнено условие А. Тогда последовательность
и выполнено условие А. Тогда последовательность 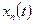 сходится к решению
сходится к решению  уравнения (1) со скоростью
уравнения (1) со скоростью 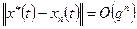 .
.
Пусть выполнено условие А и носители функций  определены в интервале
определены в интервале  .
.
Рассмотрим итерационный процесс:
 (3)
(3)
где  ,
,  - константа, определенная из условия
- константа, определенная из условия  .
.
Теорема 2. Пусть уравнение (1) имеет единственное решение  и выполнено условие А. Тогда последовательность
и выполнено условие А. Тогда последовательность 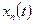 , определяемая итерационной схемой (3), сходится к решению
, определяемая итерационной схемой (3), сходится к решению  .
.
Рассмотрим итерационный процесс:
 (4)
(4)
где образ Фурье функции 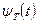 имеет вид:
имеет вид:

Теорема 3. Пусть выполнено условие А и уравнение (1) имеет единственное решение  . Тогда итерационный процесс (4) сходится при любом начальном приближении
. Тогда итерационный процесс (4) сходится при любом начальном приближении  со спектром, сосредоточенным в сегменте
со спектром, сосредоточенным в сегменте  , и справедлива оценка
, и справедлива оценка
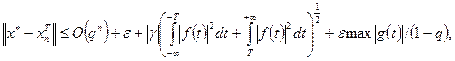 (5)
(5)
где 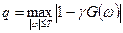 ,
, 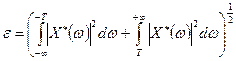 .
.
Пусть условие А не выполняется. Обозначим через 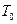 и
и 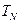 достаточно большие по абсолютной величине числа, выбор которых определяется условием
достаточно большие по абсолютной величине числа, выбор которых определяется условием  . Введем сегменты
. Введем сегменты  ,
, 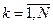 , где
, где  , таким образом, чтобы при изменении
, таким образом, чтобы при изменении  в сегменте
в сегменте  ,
, 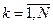 , приращение аргумента
, приращение аргумента  было меньше
было меньше 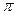 . Каждому сегменту
. Каждому сегменту  ,
, 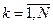 , поставим в соответствие такую константу
, поставим в соответствие такую константу 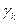 , при которой значения функций
, при которой значения функций  при
при  лежат внутри единичного круга с центром в точке
лежат внутри единичного круга с центром в точке 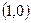 . Обозначим через
. Обозначим через  ,
, 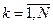 , характеристические функции сегментов
, характеристические функции сегментов  ,
, 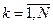 , а через
, а через 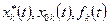 прообразы функций
прообразы функций 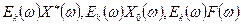 .
.
Для нахождения входного сигнала  используем итерационный процесс:
используем итерационный процесс:
 (6)
(6)
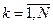 ,
, 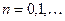 .
.
Определим 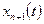 из выражения
из выражения
 (7)
(7)
Теорема 4. Пусть уравнение (1) имеет решение  . Тогда последовательные приближения
. Тогда последовательные приближения 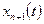 сходятся и справедлива оценка
сходятся и справедлива оценка
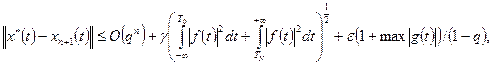
где  ,
, 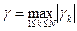 ,
,  .
.
|
|
|
|
Дата добавления: 2013-12-13; Просмотров: 372; Нарушение авторских прав?; Мы поможем в написании вашей работы!