Program Factorial;

End.

Readln (n);

Begin

Var

Program Factorial;

Комбинированный урок №14-15

Тема: Рекурсия: прямая и косвенная. Рекуррентные выражения

Цель: изучить основные понятия о рекурсии, способы применения. Дать определение рекуррентным выражениям.

Рекурсия

Рекурсивные определения как мощный аналитический аппарат используются во многих областях науки, особенно в математике.

Рассмотрим функцию факториала n!. Как правило, ее определяют как произведение первых n целых чисел: n! = 1*2*3*...*n.

Такое произведение конечно можно легко вычислить с помощью итеративных конструкций, например, оператора цикла for:

Fact: Longint;

n, i: Integer;

Write ('Введите число n: ');

Fact:= 1;

for i:= 1 to n do Fact:= Fact*i;

Writeln ('Факториал n! = ', Fact);

Однако существует также другое определение факториала, в котором используется рекуррентная формула и которое имеет такой вид:

(1) 0! = 1

(2) для любого n > 0 n! = n * (n - 1)!

Определения с помощью рекуррентных формул иногда называют рекурсивными определениями. Если для факториала первое (итеративное) определение может показаться проще, то для чисел Фибоначчи рекурсивное определение:

(1) F(1) = 1,

(2) F(2) = 1,

(3) для любого n > 2 F(n) = F(n-1) + F(n-2)

выглядит для вычислений лучше, чем прямая формула: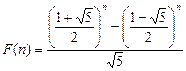

Похожие рекуррентные формулы есть также и для многих других математических определений. Понятно, что организовать вычисления по рекуррентным формулам можно и без использования рекурсии. Использование рекурсии позволяет легко (почти дословно) запрограммировать вычисления по рекуррентным формулам. Например, программа, использующая рекурсивную функцию для вычисления факториала n! имеет следующий вид:

Дата добавления: 2013-12-13