Связь систем дифференциальных уравнений с дифференциальными уравнениями высших порядков

Нормальная форма системы обыкновенных д. у. Задача Коши.

Системы обыкновенных дифференциальных уравнений.

x – независимая переменная,

y ₁(x), y ₂(x), …, y_n (x) – неизвестные (искомые) функции.

– заданные непрерывные функции от n +1 переменных в некоторой области WÍ R^{n +1}. n – порядок системы.

Решение системы: n функций

обращающих все уравнения в тождества (на интервале оси Ox).

Задача Коши: система плюс начальные условия

Теорема (осуществовании и единственности решения задачи Коши). Если

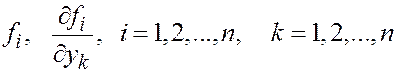
непрерывны в области W Í R^{n +1}, то

"

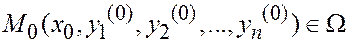
найдется интервал на оси Ox, содержащий точку x ₀, в котором $ единственное решение задачи Коши.

Определение. Если в области W Í R^{n +1}выполнены условия теоремы о$-нии и единств. решения задачи Коши, то каждое из решений при 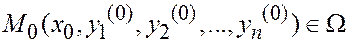называется частным решением уравнения в области W.

Общее решение: формула

такая, что

- " C ₁, C ₂, …, C_n из некоторого E Í Rⁿ она дает частные решения в W,

- каждое частное решение в W может быть получено по этой формуле выбором единственных надлежащих C ₁, C ₂, …, C_n.

Теорема. Любое д. у. n -го порядка в нормальной форме (т.е. разрешенное относительно старшей производной), может быть преобразовано в систему д. у. n -го порядка

в нормальной форме.

Доказательство.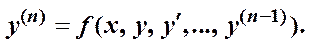

Введем n функций: y ₁(x) = y (x), y ₂(x)= y ¢(x), …,

y_n (x) = y ^{( n –1)}(x).

Þ

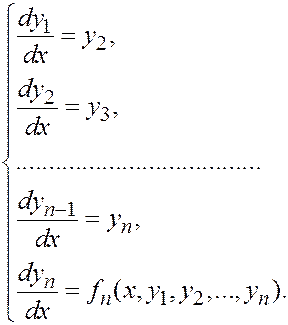
Обратно, часто удается решение системы д. у. n -го порядка в нормальной форме свести к решению одного дифференциального уравнения n -го порядка.

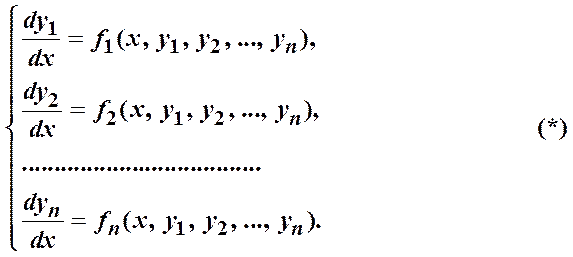
Выберем функцию y ₁(x). Для нее будем получать д.у. порядка n.

Дифференцируем первое уравнение n –1 раз, заменяя на каждом шаге появляющиеся производные y ₂¢(x), …, y_n ¢(x) правыми частями уравнений системы.

Получим новую систему:

Если удастся выразить из первых n –1 уравнений y ₂, …, y_n через y ₁, y ₁¢, …, y ₁^{( n –1)} (решая систему n –1 алгебраических уравнений с n –1 неизвестными), то подставим их в последнее уравнение и получим уравнение n- го порядка относительно y ₁(x).

Дата добавления: 2013-12-13