Статическая сторона задачи

Рис.2.52

Пример 24.

Рис. 2.51

Геометрическая сторона задачи.

Статическая сторона задачи.

Решение.

Рис.2.50

Пример 23.

Определить усилия в стержнях системы, возникающие в результате поворота двухсторонней винтовой стяжки <<С>> на угол 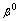. Жесткость стяжки равна жесткости третьего стержня (рис. 2.50).

Дано: E₁=E₂=E₃=E, F₁=2F₃=2F₂=2F; шаг винтовой нарезки гайки- h; l₁=l.

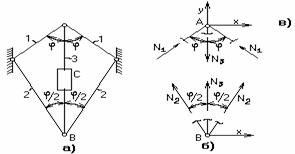
Составляем уравнения равновесия узла А (рис. 2.50, в). Учитывая симметрию относительно оси Y, имеем:

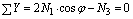
отсюд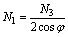а (а)

Составляем уравнения равновесия узла B (рис. 2.50, с).

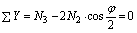
отсюда 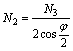(b)

Тогда степень статической неопределенности подсчитывается так: S =3-2=1

При повороте гайки на угол 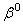стержень 3, состоящий из двух частей, ввинтится в гайку на величину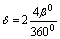

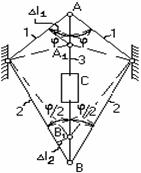
За счет ввинчивания стержня 3 точки А и В сблизятся на величину 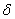, а за счет растяжения этого стержня и стяжки они разойдутся на величину 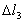(рис. 2.51). Тогда, на основании схемы деформированной системы, ус­ловие совместности деформаций будет иметь вид:

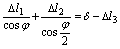(с)

3. Физическая сторона задачи.

Согласно закону Гука.

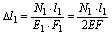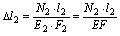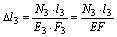; ; (d)

Здесь l ₁= l ₂ по условию, а l ₂ и l ₃ можно определить из равенства проекций стержней на горизонтальную и вертикальную оси (рис. 2.50, а):

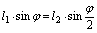
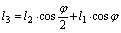
Подставляя (d) в (с), получим:

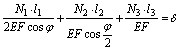(е)

4. Определение неизвестных.

Решая систему, составленную из уравнений (а), (в) и (е), получим:

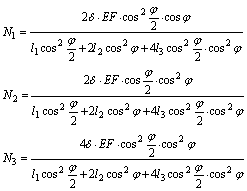
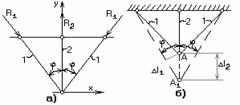
Определить усилия в стержнях системы, возникающие в результате повышения температуры всех стержней на 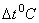(рис. 2.52, а)

Дано: F₁=F₂=F; E₁= 0,5 E; E₂=E; 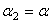; ; 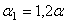l₁=l

Решение.

С учетом симметрии относительно оси Y имеем:

,

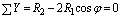отсюда 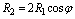(a)

2. Геометрическая сторона задачи.

В результате термического расширения точка А переместится в А₁ (рис. 2.52, б).Исходя из схемы деформированной конструкции можно составить условие совместности деформаций:

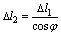(b)

3. Физическая сторона задачи.

Крайние стержни 1 длиннее среднего стержня 2; кроме того, у край­них стержней коэффициент линейного расширения больше, чем у сред­него. По этой причине точка А у первых стержней опустилась бы ниже, чем точка А у второго стержня, если бы они деформировались отдельно. Но так как они в точке А связаны шарниром, то возникает силовое взаи­модействие боковых и среднего стержней. Боковые стержни, удлиняясь за счет термического воздействия, будут одновременно укорачиваться в результате действия возникающего усилия, средний же стержень будет удлиняться как за счет термического расширения, так и за счет механи­ческого действия на него крайних стержней.

Следовательно

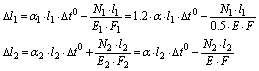(c)

где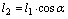

подставляя (с) в (б), получим:

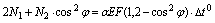(d)

4. Определение неизвестных.

Решая систему уравнений (а) и (d) с учетом, что R₁=N₁ и R₂=N₂, получим:

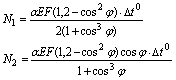
Дата добавления: 2013-12-13