Расчет конструкций по допускаемым нагрузкам

Рис.2.55

Рис. 2.54

1. Найдем усилия и напряжения в стержнях, выразив их через силу Q.

Статическая сторона задачи. По условию задачи необходимо определить усилия N ₁, и N ₂ стальных стержней АА ₁, и ВВ ₁, a в определений реакций Н_К, и R_К нет необходимости. Поэтому достаточно из трех возможных уравнений равновесия использовать одно, в которое не входили бы реакция Н_К, и R_К. Таким является уравнение в виде суммы моментов всех сил относительно шарнира К:

,

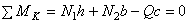где 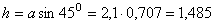м.

Подставляя в уравнение значения h, b, с, получим

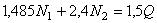. (а)

Геометрическая сторона задачи. Под действием внешней силы Q абсолютно жесткий брус повернется вокруг точки К. Шарниры А и В после деформации переходят в положение А ₂ и В ₂ соответственно, т.е. перемещаются по вертикали на величины 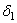и (рис.2.55).

Из подобия треугольников AA ₂ К и ВВ ₂ К находим

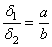. (b)

Выразим укорочение 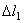стержня АА ₁ и удлинение стержня ВB ₁, через перемещения 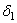и .

, ,

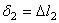откуда

или с учетом равенства (b)

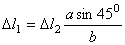(c)

Физическая сторона задачи. Используя закон Гука, записанный для абсолютных деформаций, выразим удлинения стержней через усилия

;

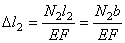; (d)

Подставим выражения (c) в условие (d)

,

после сокращения получим

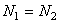(e)

Решаем совместно уравнения статики (a) и уравнение (e):

.

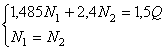
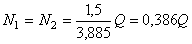Определяем напряжения в стержнях 1 и 2:

Па,

Па.

2. Найдем допускаемую нагрузку [ Q ], приравняв большее из напряжений в двух стержнях допускаемому напряжению 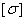= 160 МПа.

,

откуда

Н.

3. Найдем предельную грузоподъемность системы Q_{пр .} и допускаемую нагрузку [ Q_пр ], если предел текучести = 240 МПа и запас прочности n = 1,5.

При увеличении нагрузки Q cверх значения [ Q ] напряжения в обоих стержнях сначала увеличивается прямо пропорционально нагрузке. При увеличении нагрузки до некоторой величины напряжение 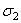во второй стержне достигают предела текучести , а усилие N ₂ - предельного значения N _{2 пр} = c ₁· F. При этом напряжение 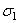в первом стержне остается меньше . В процессе дальнейшего увеличения нагрузки напряжения во втором стержне остаются постоянными, равными пределу текучести, а в первом - возрастают, пока также не становятся равными , усилие N ₁ при этом равно 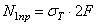. Это состояние системы называется предельным, соответствующим исчерпанию ее грузоподъемности. Дальнейшее, даже незначительное увеличение нагрузки связано с весьма большими деформациями системы. Величину Q, вызываюшую предельное состояние, обозначают Q_пр и называют предельной нагрузкой.

Для определения Q_пр, подставим в уравнение (a) значения сил, соответствующих предельному состоянию, когда Q = Q_пр, N ₁ = N _{1 пр} , N ₂ = N _{2 пр} :

,

откуда

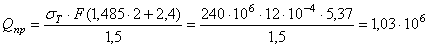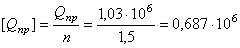Н.

Н.

4. Сравним величины допускаемых нагрузок [ Q ] и [ Q_пр ]

.

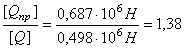Следовательно, при расчете на прочность данной системы по предельной нагрузке грузоподъемность ее увеличивается на 38%.

Дата добавления: 2013-12-13