Решение. Построить эпюры для стержня, изображенного на рисунке, при нагружении силой P и равномерно распределенной нагрузкой q

Пример 20.

Построить эпюры для стержня, изображенного на рисунке, при нагружении силой P и равномерно распределенной нагрузкой q. Составить условие прочности.

а) в) г)

1. Определение опорной реакции

Уравнение равновесия сил (рис. а)

,

откуда .

2. Определение внутренних усилий методом сечений

Стержень содержит два участка с разным характером нагружения. На первом участке делаем сечение на расстоянии 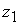и из условия равновесия левой отсеченной части находим (рисунок 1, б)

.

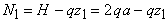Следовательно, на первом участке график-эпюра прямая линия.

Строим эпюру по двум точкам. При имеем 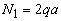, а при получаем .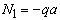

На втором участке отсекаем на расстоянии правую часть стержня. Действие левой части на правую заменяем усилием (рис. б). Из уравнения равновесия отсеченной части правой части находим

.

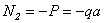Следовательно, на втором участке 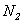имеем постоянное значение.

Эпюра приведена на рис. в. На расстоянии усилие . Найдем это расстояние:

; .

Максимальное значение 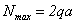возникает в защемлении. Это сечение является опасным по прочности.

Контроль правильности построенной эпюры осуществляется с помощью правил дифференциальной зависимости Д. Журавского

:

1) на незагруженном участке и ;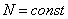

2) на равномерно загруженном участке и , т.е. эпюра − прямая линия, возрастающая с ростом , если угловой коэффициент

, и убывающая, если .

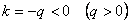Оба правила в нашей задаче соблюдены.

3. Расчет на прочность

Условие прочности стержня

.

Пусть поперечное сечение стержня − прямоугольное с соотношением сторон . Тогда .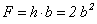

Допускаемое напряжение (дерево), , . Требуется определить размеры поперечного сечения h и b. Тогда:

,

откуда .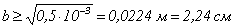

Округляем значение 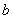до значения 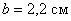, тогда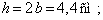 . Проверяем стержень на прочность с подобранными размерами поперечного сечения:

,

что больше допустимого значения .

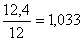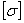Перенапряжение составит , т.е. . Отклонение от допускается в пределах .

4. Построение эпюры перемещений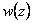

На первом участке:

,

или

.

Эпюра – парабола. В сечении , где , перемещение достигает максимального значения:

.

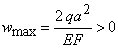Выпуклость параболы определяется знаком второй производной 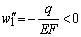, т.к. 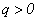. Следовательно, кривая перемещений обращена выпуклостью к верху.

При имеем

.

На втором участке получаем

.

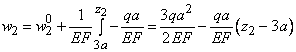Эпюра − прямая линия. При 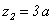имеем , а при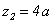

.

Строим прямую линию на втором участке (рис. г). Задача решена.

Дата добавления: 2013-12-13