
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Главная
|
|
|
|
Задача № 57
Задача № 56
Задача № 55
Задача № 54
Задача № 53
Задача № 52
Задача № 51
Задача № 50
Задача № 49
Задача № 48
Задача № 47
Задача № 46
Задача № 45
Задача № 44
Задача № 43
Задача № 42
Задача № 41
Задача № 40
Задача № 39
Задача № 38
Задача № 37
Задача № 36
Задача № 35
Задача № 34
Задача № 33
Задача № 32
Задача № 31
Задача № 30
Задача № 29
Задача № 28
Задача № 27
Задача № 26
Задача № 25
Задача № 24
Задача № 23
Задача № 22
Задача № 21
Задача № 20
Задача № 19
Задача № 18
Задача № 17
Задача № 16
Задача № 15
Задача № 14
Задача № 13
Задача № 12
Задача № 11
Задача № 10
Задача № 9
Задача № 8
Задача № 7
Задача № 6
Задача № 5
Задача № 4
Задача № 3
Задача № 2
Задача №1
Задачи для самостоятельного решения
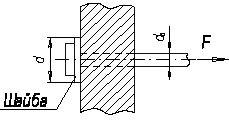
Стяжка диаметром 25 мм растянута усилием F (см. рисунок), вызывающим в ней напряжение 100 МПа. Чему должен равняться диаметр шайбы d, чтобы давление, передаваемое ею на стену, не превышало 1,4 МПа?
Ответ: 213 мм
Медная проволока диаметром 1,2 мм удлиняется на 0,25 мм под нагрузкой 90 Н. Определить длину проволоки.
Ответ: 314 мм.
Стержень из малоуглеродистой стали шириной 0,3 м и толщиной 0,015 м ослаблен заклепочным отверстием диаметром 0,023 м, расположенным на оси стержня. Какое растягивающее усилие этот стержень может выдержать, если допускаемое напряжение равно 90 МПа?
Ответ: 374 кН.
Определить напряжения во всех участках изображенного на рисунке стального стержня и полную его деформацию, если поперечное сечение равно 1∙10-3 м2.
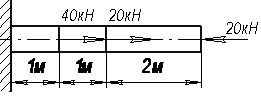
Ответ: на левом участке 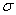 =40 МПа; на среднем
=40 МПа; на среднем 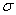 = 20 МПа; на правом
= 20 МПа; на правом 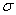 = -20 МПа;
= -20 МПа; 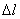 = 0.
= 0.
Стальная полоса (см. рисунок) растянута продольными силами. Она ослаблена круглыми заклепочными отверстиями, как показано на рисунке. Определить среднюю величину напряжений в опасном сечении.
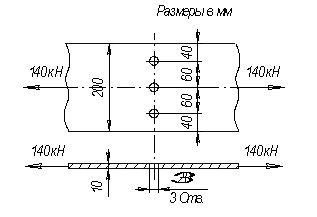
Ответ: 100 МПа.
К нижнему концу троса, закрепленного верхним концом, подвешен груз F = 75 кН. Трос составлен из проволок диаметром d = 2 мм. Допускаемое напряжение для материала троса равно [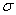 ] = 300 МПа. Из какого количества проволок должен быть составлен трос?
] = 300 МПа. Из какого количества проволок должен быть составлен трос?
Ответ: 80 проволок.

Определить напряжения в обеих частях изображенного на рисунке стержня, а также полное его удлинение. Материал стержня — сталь, сечение круглое.
Ответ: в левой части 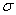 =127,6 МПа; в правой
=127,6 МПа; в правой 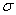 =31,9 МПа;
=31,9 МПа; 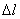 = 0,575 мм.
= 0,575 мм.
Определить напряжение в шатуне автомобильного двигателя, поперечное сечение I – I которого (см. рис.) имеет форму двутавра, и проверить прочность при допускаемом напряжении [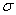 ] = 140 МПа. Найти число шпилек n для крепления головки цилиндра, если внутренний диаметр резьбы d В = 8 мм, [
] = 140 МПа. Найти число шпилек n для крепления головки цилиндра, если внутренний диаметр резьбы d В = 8 мм, [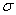 ]=80 МПа. Диаметр цилиндра D = 80 мм, давление газов р = 3,6 МПа.
]=80 МПа. Диаметр цилиндра D = 80 мм, давление газов р = 3,6 МПа.

Ответ. Напряжение  = 144 МПа,
= 144 МПа, 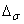 = 2,85%, что допустимо, число шпилек п = 5.
= 2,85%, что допустимо, число шпилек п = 5.

Определить допускаемую нагрузку для стального листа толщиной t =10 мм, если допускаемое напряжение [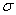 ] = 100 МПа (см.рис.), размеры в миллиметрах.
] = 100 МПа (см.рис.), размеры в миллиметрах.
Ответ. Допускаемая нагрузка [F]= 140 кН.
Определить напряжение в точке О, а также величину растягивающей силы F, зная напряжение в точке К, равное 100 МПа.

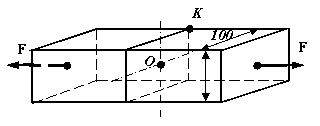
При растяжении стержня силой F = 800 кН в точке К с координатами Х к = 4 см и У к = 3 см возникает напряжение 160 МПа. Чему равен диаметр стержня?
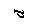

Как изменится абсолютное удлинение бруса, если:
а) увеличить линейные размеры b и l в 2 раза;
б) увеличить длину l в 2 раза и заменить материал (например, медь на сталь);
в) уменьшить размер b в 2 раза, длину l в 4 раза и заменить материал (например, сталь на титан);
г) уменьшить в 3 раза линейные размеры b, l и силу F?

Вертикально подвешенный резиновый жгут под действием некоторого груза, прикрепленного к нижнему свободному концу, удлиняется на 16 см. Затем он дважды складывается пополам и к сложенному таким образом жгуту прикладывается тот же самый груз. Насколько удлинится жгут в этом случае?
Жесткость стального провода равна 10 Н/мм. Чему равно удлинение троса, сплетенного из 10 таких проводов, если к концу троса подвесить груз весом 2 кН?
При буксировке автомобиля массы 1т результирующая сил сопротивления и трения в 50 раз меньше веса автомобиля. Чему равна жесткость троса, если при равномерном движении автомобиля трос удлиняется на 20 мм?
Определить ширину фундамента здания, учитывая, что среднее напряжение в грунте не должно превышать 0,5 МПа. Общий вес фундамента, стены и полезной нагрузки на 1 м длины здания равен 500 кН/м.
Какую нагрузку сможет выдержать короткая гранитная колонна диаметром 80 см, если допускаемое напряжение на сжатие гранита равно [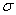 ] = 4 МПа?
] = 4 МПа?
Стальной стержень кругового поперечного сечения растягивается силой 100кН. При каком наименьшем диаметре стержня относительное удлинение не превышает 5·10-4, а напряжение – 120 МПа?
При какой минимальной базе тензометра с коэффициентом увеличения 1000 и точностью отсчета 0,1 мм можно обеспечить измерение напряжений в стальной детали с точностью не менее 1 МПа?
Стальной стержень кругового поперечного сечения диаметром 30 мм растянут на испытательной машине силой 120 кН. Его продольное удлинение, замеренное на длине 50 мм, составило 42 мкм, а изменение диаметра – 7 мкм. Определить модуль упругости и коэффициент Пуассона материала стержня.
Для установки тяжелой колонны в вертикальное положение требуется поднять ее левый конец. К какой точке колонны нужно прикрепить трос, чтобы напряжения в нем были минимальными? Выполнить проверку прочности троса при следующих данных: вес колонны G = 200 кН, ее длина l = 16 м, высота опоры Н = 4 м, площадь поперечного сечения троса А = 24 см2, допускаемое напряжение [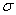 ] =170 МПа.
] =170 МПа.

Для заданных брусьев построить эпюры продольных сил, напряжений и перемещений. Определить наибольшие напряжения, перемещения и запасы по текучести, полагая F = qu = 10 кН, А = 2 см2, а = 20 см, 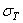 = 200 МПа, Е = 100 ГПа.
= 200 МПа, Е = 100 ГПа.
Трещины в асфальтированных дорогах возникают чаще всего зимой. Почему?
Чтобы стакан не лопнул при наполнении его кипятком, рекомендуется в него предварительно опустить чайную ложку и лить кипяток на ложку. какую роль играет в данном случае чайная ложка?
На некоторых железных дорогах сваривают рельсы в одну непрерывную нитку. Спрашивается, в каком интервале температур должна быть произведена сварка, чтобы при колебаниях температур от минус 40оС до плюс 40оС наибольшие сжимающие напряжения не превышали 75 МПа, а наибольшие растягивающие – 150 МПа, если Е=200 ГПа,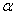 =125
=125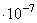 ?
?
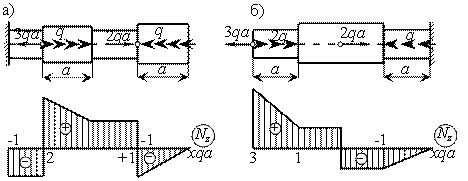
Эпюры Nz для стержней, представленных на рисунке предлагается построить самостоятельно. Для проверки тут же дается решение.
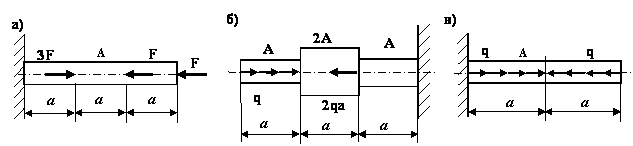
Подобрать диаметр бруса, если F 1=3 кН; F 2=5 Кн; F 3=16кН и  =140 МПа.
=140 МПа.
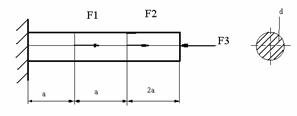
Силу перенести по линии её действия из точки “ B ” в точку “ C ”. Что при этом изменится?

Найти продольные силы N на участках стержня, построить эпюру, вычислить напряжения во всех участках представленного на рисунке стального стержня и полную его деформацию. Сила Р = 20 кН, а = 1 м, площадь поперечного сечения стержня F= 5 см2.

Ответ: На участках слева на право 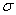 = 80 МПа,
= 80 МПа, 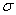 = 0,
= 0, 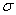 = - 40 МПа,
= - 40 МПа, 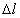 = 0.
= 0.
Построить эпюры нормальных сил и нормальных напряжений для бруса постоянного поперечного сечения с А = 10 см2. На брус действует внешняя распределенная осевая нагрузка q = 5 кН/м и продольные сосредоточенные силы F = 15 кН(рис. а).

Ответ: эпюры нормальных сил и напряжений представлены на рис. б, в.
Построить эпюры нормальных сил и нормальных напряжений для бруса постоянного поперечного сечения с А = 10 см2. На брус действует внешняя распределенная осевая нагрузка q = 5 кН/м и продольные сосредоточенные силы F = 15кН(рис. а).
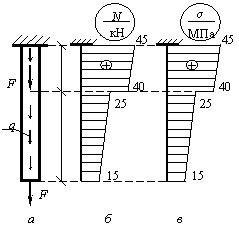
Ответ: правильные результаты показаны на рис. б, в.
Дан прямой стальной стержень кусочно - постоянного сечения, для которого a = 0,4 м, а площади поперечных сечений указаны на рис. а.







































 Построить эпюры нормальных сил и нормальных напряжений. Найти сечение, где действует
Построить эпюры нормальных сил и нормальных напряжений. Найти сечение, где действует 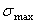 .
.

Ответ: эпюры нормальных сил и нормальных напряжений при учете только собственного веса стального стержня представлены на рис. б, в,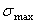 = 1,3345 кг/см2в точке С участка с площадью поперечного сечения А 2.
= 1,3345 кг/см2в точке С участка с площадью поперечного сечения А 2.
Проверить прочность стального стержня, изображенного на рис. а. Материал – сталь с Ry = 2450 кг/см2и объемным весом 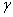 = 0,00785 кг/см3, F = 10 т,
= 0,00785 кг/см3, F = 10 т, 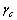 = 1.
= 1.

Ответ: 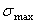 = 1429 кг/см2 < Ry = 2450 кг/см2 (см. рис. в), следовательно, условие прочности выполняется.
= 1429 кг/см2 < Ry = 2450 кг/см2 (см. рис. в), следовательно, условие прочности выполняется.
Построить эпюру нормальных сил для стержня замоноличенного в массив (рис. а), предполагая, что интенсивность сил трения постоянна по длине a. Собственным весом стержня пренебречь.

Ответ: эпюра нормальных сил показана на рис. б.
Определить площади верхнего Ав0 и нижнего Ав1 сечений, а также вес кладки из глиняного кирпича в форме бруса равного сопротивления сжатию, если на верхнее сечение действует сосредоточенная сила F = 3000 кН, высота стойки l = 20 м, R = 1,5 МПа;  = 1,00. Объемный вес кладки принять
= 1,00. Объемный вес кладки принять 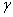 = 18 кН/м3.
= 18 кН/м3.
Ответ: Ав0 = 2 м2; Ав1 = 2,54 м2; стойка из глиняного кирпича объемом 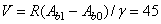 м3 весит
м3 весит 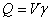 = 810 кН.
= 810 кН.
Получить аналитические выражения для определения напряжений в поперечных сечениях бруса, имеющего форму, показанную. на рисунке. Толщину бруса принять постоянной и равной t = 2 см. Требуется: а) решить задачу, учитывая только собственный вес бруса с 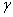 = 78,5 кН/м3, а сжимающую силу F принять равной нулю (F = 0); б) решить задачу без учета собственного веса, но принять F = 200 кН; в) решить задачу, принимая F = 200 кН и, учитывая собственный вес стального бруса с
= 78,5 кН/м3, а сжимающую силу F принять равной нулю (F = 0); б) решить задачу без учета собственного веса, но принять F = 200 кН; в) решить задачу, принимая F = 200 кН и, учитывая собственный вес стального бруса с 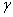 = 78,5 кН/м3.
= 78,5 кН/м3.

Ответ: а)  , [Па]; б)
, [Па]; б)  , [Па]; в)
, [Па]; в) 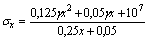 , [Па].
, [Па].
Стальной стержень квадратного сечения со сторонами ai, находится под воздействием сосредоточенных сил Fi, направленных вдоль оси стержня (рис. а).

Определить размеры поперечных сечений стержня так, чтобы в любом сечении стержня действовали нормальные напряжения, равные расчетному сопротивлению Ry = 240 МПа. Собственный вес стержня не учитывать.
Ответ: a 1 =0,91см; a 2 = 1,02 см; a 3 = 1,29 см; a 4 = 1,12 см (рис. б).
Определить допускаемую нагрузку Fadm растягиваемого стального листа, ослабленного отверстиями d = 2 см (см. рис.). Расчетное сопротивление стали принять Ry = 240 МПа, а  = 1. Толщина листа t =1 см, ширина b = 15 см.
= 1. Толщина листа t =1 см, ширина b = 15 см.

Ответ: Fadm = 216 кН.
Определить допускаемую нагрузку Fadm растягиваемого стального листа, ослабленного отверстиями d = 2 см (см. рис.). Расчетное сопротивление стали принять Ry = 240 МПа, а 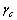 = 1. Толщина листа t = 1 см, ширина b = 13 см.
= 1. Толщина листа t = 1 см, ширина b = 13 см.

Ответ: Fadm = 216 кН.
Определить допускаемую толщину t растягиваемого стального листа, изображенного на рисунке, если диаметры отверстий d = 2 см, а ширина листа b = 20 см. Расчетное сопротивление стали принять: Ry = 240 МПа, а 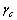 = 1. Внешняя растягивающая сила F = 20 т.
= 1. Внешняя растягивающая сила F = 20 т.

Ответ: 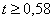 см.
см.
В стенке стального двутавра № 20 вырезано отверстие диаметром d = 10 см (см. рис.).Определить допускаемую на-грузку Fadm, которая может быть приложена вдоль продольной оси ослабленного двутавра. Расчетное сопротивление стали принять Ry = 2450 кг/см2, а γc = 1,1.
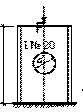
Ответ: Fadm = 571 кН.
В стенке стального двутавра № 20 вырезано отверстие диаметром d = 10 см. Определить допускаемую равномерно распределенную нагрузку  (кг/м), которую можно приложить вдоль стенки двутавра (см. рис.). Расчетное сопротивление стали Ry = 2450 кг/см2, а
(кг/м), которую можно приложить вдоль стенки двутавра (см. рис.). Расчетное сопротивление стали Ry = 2450 кг/см2, а 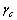 = 1.
= 1.

Ответ:  = 84933 кг/м = 833,19 Н/м.
= 84933 кг/м = 833,19 Н/м.
Определить перемещение нижнего конца стержня, изображенного на рисунке. Дан прямой стержень кусочно-постоянного сечения, для которого a 1 = 25 см, a 2 = 15 см, a 3 = 10 см, a 4 = 20 см, А 1 = А = 20 см2, А 2 =А 3 =4 А, А 4 = 2 А. Стержень находится под действием сосредоточенных сил F 1 = 327,2 Н; F 2 = 1 кН; F 3 = 500 Н и собственного веса с 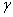 = 78,5 кН/м3, действующих вдоль оси стержня. Принять
= 78,5 кН/м3, действующих вдоль оси стержня. Принять 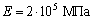 .
.

Ответ: 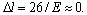
Определить перемещение нижнего конца стержня, представленного на рисунке. Принять а = 0,4 м; объемный вес материала стержня 

Ответ: 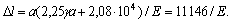
Определить линейную продольную деформацию каждого участка стержня кусочно-постоянного квадратного сечения, изображенного на рисунке. Вычислить перемещение точки С рассматриваемого стержня и построить эпюру перемещений поперечных сечений стержня. Принять a 1 = 0,9 см; a 2 = 1 см; a 3 = 1,3 см; a 4 = 1,1 см.Задачу решить без учета собственного веса стержня, 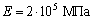 .
.
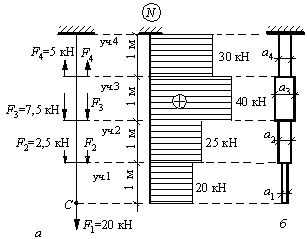
Ответ:  мм;
мм; 
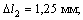

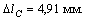
Стержень постоянного поперечного сечения нагружен сосредоточенными силами (см. рис. а). Построить эпюру перемещений. Собственный вес стержня в расчете не учитывать.
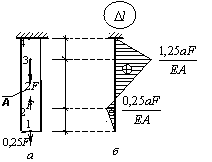
Ответ: эпюра перемещений показана на рис. б.
Прямой стальной стержень с площадью поперечного сечения А = 5 см2 закреплен верхним концом, а к нижнему концу приложена растягивающая сила F =30 кН. Определить относительную и продольную линейную деформации, относительную поперечную деформацию  , если длина стержня l = 3 м, модуль Юнга
, если длина стержня l = 3 м, модуль Юнга 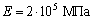 , коэффициент Пуассона
, коэффициент Пуассона 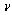 = 0,3; удельный вес материала стержня
= 0,3; удельный вес материала стержня 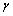 = 78,5 кН/м3.
= 78,5 кН/м3.
Ответ:  0,9 мм;
0,9 мм; 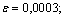
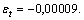
Определить относительную деформацию в каждом участке стержня постоянного поперечного сечения, показанного на рисунке. Собственным весом стержня при расчете пренебречь.
Ответ: 
Стальной вертикальный стержень из двутавра № 30 растягивается под действием собственного веса. Длина стержня l = 20 м. Определить нормальное напряжение в закрепленном верхнем конце и перемещение 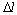 нижнего конца стержня,
нижнего конца стержня, 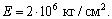
Ответ: 
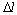 = 0,00785 см.
= 0,00785 см.
Вертикальный стержень из двух швеллеров № 20, закрепленный верхним концом, растягивается под действием собственного веса и силы F = 40 т. Определитьмаксимальное нормальное напряжение и перемещение 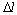 нижнего конца стержня при модуле продольной упругости
нижнего конца стержня при модуле продольной упругости 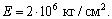 Длина стержня l =4 м. Сила приложена к нижнему концу стержня.
Длина стержня l =4 м. Сила приложена к нижнему концу стержня.
Ответ: 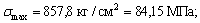
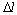 =0,171 см.
=0,171 см.
Стальной болт длиной l = 16 см при затяжке получил удлинение 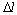 = 0,12 мм. Определить напряжение в болте, если модуль Юнга
= 0,12 мм. Определить напряжение в болте, если модуль Юнга 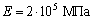 .
.
Ответ: 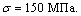
Алюминиевый стержень круглого поперечного сечения диаметром 10 см растягивается силой F. Найти величину допускаемой силы Fadm, если допускаемое уменьшение начального диаметра 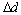 =0,002см; коэффициент Пуассона
=0,002см; коэффициент Пуассона 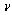 = 0,35.
= 0,35.
Ответ: Fadm = 283 кН.
Дан прямой стержень кусочно-постоянного сечения, для которого a 1 = 25 см, a 2 = 15 см, a 3 = 10 см, a 4 = 20 см, А 1 = А = 20 см2, А 2 =А 3 =4 А. А 4 = 2 А (рис. а). Стержень находится под действием сосредоточенных сил F 1 = 327,2 Н; F 2 = 1 кН; F 3 = 500 Н и собственного веса с 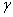 = 78,5 кН/м3, действующих вдоль оси стержня.
= 78,5 кН/м3, действующих вдоль оси стержня.
Требуется построить для заданного стержня эпюры нормальных сил и нормальных напряжений.
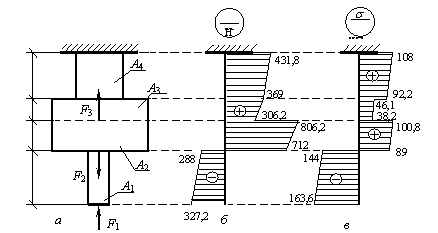
Ответ: правильный результат показан на рис. б, в.
Дан прямой стальной стержень кусочно-постоянного сечения, для которого а = 0,4 м, а площади поперечных сечений указаны на рис. а. При учете действия только собственного веса стального стержня эпюры нормальных сил и напряжений имеют вид, показанный на рис. б, в.
Как изменятся эпюры нормальных сил и напряжений, если рассмотреть тот же стержень, но с защемленными обоими концами. Проверить правильность вычислений, используя критерий равенства площадей эпюры 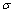 с разными знаками. Найти поперечное сечение, где N = 0,
с разными знаками. Найти поперечное сечение, где N = 0, 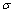 = 0.
= 0.
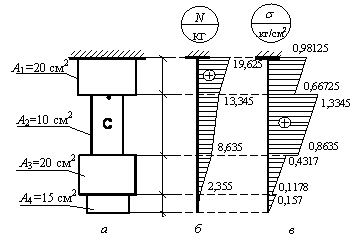
Ответ: опорная реакция нижней опоры R = –9,83 кг, следовательно, соответствующие значения эпюры N, показанной на рис. б, необходимо сложить с величиной R = –9,83 кг.
Имеются две стальные трубы, одна из которых имеет наружный диаметр D 1 = 102 мм и толщину стенки t 1 = 3 мм, а другая – D 2= 168 мм, t 2= 4 мм (см. рис.). Используя справочные данные в сортаменте можно определить, что площади их поперечных сечений равны A 1 = 9,3 см2; A 2 = 20,6 см2. Обе трубы имеют длину l = 20 см. Вставленные осесимметрично друг в друга трубы подвергаются сжатию силой F = 20 т. Определить нормальные силы и напряжения, передающиеся на каждую трубу.
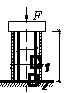
Ответ: 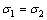 = 668,9 кг/см2 = 65,62 МПа; N 2= 13779,3 кг =135,2 кН; N 1 = 6220,7 кг = 61 кН.
= 668,9 кг/см2 = 65,62 МПа; N 2= 13779,3 кг =135,2 кН; N 1 = 6220,7 кг = 61 кН.
Имеются две трубы, одна из которых стальная с наружным диаметром D 1 = 102 мм и толщиной стенки t 1 = 3 мм(А 1 = 9,3 см2), а другая алюминиевая с наружным диаметром D 2 = 168 мм и t 2 = 4 мм (А 2 = 20,6 см2). Вставленные осесимметрично друг в друга трубы подвергаются сжатию силой F = 20 т (см. рис.). Определить нормальные силы и напряжения, передающиеся на каждую трубу. Вычислить укорочение труб (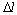 ), если их длина l = 20 см, а модуль продольной упругости для алюминия
), если их длина l = 20 см, а модуль продольной упругости для алюминия  , для стали – Е 1 = 2,1·106 кг/см2.
, для стали – Е 1 = 2,1·106 кг/см2.
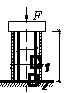
Ответ: N 1= 11,925 т = 116,98 кН; 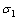 = 1282 кг/см2 = 125,76 МПа; N 2= 8,075 т = 79,21 кН;
= 1282 кг/см2 = 125,76 МПа; N 2= 8,075 т = 79,21 кН;  = 392 кг/см2 = 38,45 МПа;
= 392 кг/см2 = 38,45 МПа; 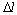 = 0,12 мм.
= 0,12 мм.
Дана конструкция, состоящая из трех элементов: двух труб разного диаметра и одного сплошного стержня (см. рис.). Все три элемента выполнены из разных материалов с модулями продольной упругости Е 1, Е 2, Е 3. Площади поперечных сечений двух труб А 2 и А 3, а площадь поперечного сечения сплошного стержня А 1. Элементы осесимметрично вставлены один в другой и помещены между абсолютно жесткими плитами. Вся стержневая система сжимается силой F. Требуется определить нормальные напряжения в поперечных сечениях каждого из элементов конструкции.

Ответ: 


|
|
|
|
Дата добавления: 2013-12-13; Просмотров: 3336; Нарушение авторских прав?; Мы поможем в написании вашей работы!