Геометрический способ сложения сил

Рис.13

Рис. 12

Проекция силы на ось и на плоскость.

Лекция 2. Равновесие системы сил. Пара сил.

В данной лекции рассматриваются следующие вопросы

1. Проекция силы на ось и на плоскость.

2. Геометрический способ сложения сил.

3. Равновесие системы сходящихся сил.

4. Момент силы относительно центра или точки.

5. Теорема Вариньона о моменте равнодействующей.

6. Пара сил.

7. Момент пары.

8. Свойства пар.

9. Сложение пар.

10. Теорема о параллельном переносе силы.

11. Приведение плоской системы сил к данному центру.

12. Условия равновесия произвольной плоской системы сил.

13. Случай параллельных сил.

14. Решение задач.

Изучение этих вопросов необходимо в дальнейшем для изучения центра тяжести, произвольной пространственной системы сил, сил трения скольжения, моментов трения качения, решения задач в дисциплине «Сопротивление материалов».

Перейдем к рассмо­трению аналитического (численного) метода решения задач статики. Этот метод основывается на понятии о проекции силы на ось. Как и для всякого другого вектора, проекцией силы на ось называется скалярная величина, равная взятой с соответствующим знаком длине отрезка, заключенного между проекциями начала и конца силы. Проекция имеет знак плюс, если перемещение от ее начала к концу происходит в положительном направлении оси, и знак минус - если в отрицательном. Из определения следует, что проек­ции данной силы на любые параллельные и одинаково направлен­ные оси равны друг другу. Этим удобно пользоваться при вычисле­нии проекции силы на ось, не лежащую в одной плоскости с силой.

Обозначать проекцию силы на ось Ох будем символом . Тогда для сил, изображенных на рис. 12, получим:

, .

Но из чертежа видно, что , .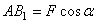

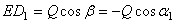Следовательно,

, ,

т. е. проекция силы на ось равна произведению модуля силы на косинус угла между направлением силы и положительным на­правлением оси. При этом проекция будет положительной, если угол между направлением силы и положительным направлением оси - острый, и отрицательной, если этот угол - тупой; если сила перпен­дикулярна к оси, то ее проекция на ось равна нулю.

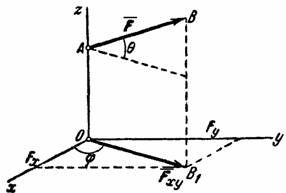
Проекцией силы на плоскость Оху называется вектор , заключенный между проекциями начала и конца силы на эту плоскость (рис. 13). Таким образом, в отличие от проекции силы на ось, проекция силы на плоскость есть величина векторная, так как она характеризуется не только своим чис­ленным значением, но и направлением в плоскости Оху. По модулю 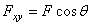, где — угол между направ­лением силы и ее проекции .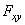

В некоторых случаях для нахож­дения проекции силы на ось бывает удобнее найти сначала ее проекцию на плоскость, в которой эта ось ле­жит, а затем найденную проекцию на плоскость спроектировать на данную ось. Например, в случае, изображенном на рис. 13, найдем таким способом, что

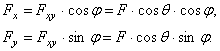
Решение многих задач механики связано с известной из векторной алгебры операцией сложения векторов и, в частности, сил. Величину, равную геометрической сумме сил какой-нибудь системы, будем называть главным вектором этой системы сил. Понятие о геометрической сумме сил не следует смешивать с понятием о равнодействующей, для многих систем сил, как мы увидим в дальнейшем, равнодействующей вообще не существует, геометрическую же сумму (главный вектор) можно вычислить для любой системы сил.

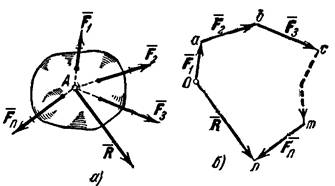
Геометрическая сумма (главный вектор) любой системы сил определяется или последовательным сло­жением сил системы по правилу параллелограмма, или построением силового многоугольника. Второй способ является более простым и удобным. Для нахождения этим способом суммы сил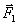, , 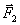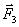…, 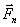(рис. 14, a), откладываем от произвольной точки О (рис. 14, б) век­тор Oa, изображающий в выбранном масштабе cилу F ₁, от точки a откладываем вектор , изображающий силу F ₂, от точки b откла­дываем вектор bc, изображающий силу F ₃ и т. д.; от конца m пред­последнего вектора откладываем вектор mn, изображающий силу F _n.Соединяя начало первого вектора с концом последнего, получаем вектор = 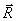, изображающий геометрическую сумму или главный вектор слагаемых сил:

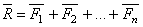или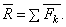

От порядка, в котором будут откладываться векторы сил, модуль и направление 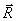не зависят. Легко видеть, что проделанное по­строение представляет собою результат последовательного приме­нения правила силового тре­угольника.

Дата добавления: 2013-12-13