Решение. Для сложных составных поперечных сечений, не содержащих осей симметрии, предлагается следующий порядок расчета

Пример 7.

Пример 6.

Для сложных составных поперечных сечений, не содержащих осей симметрии, предлагается следующий порядок расчета.

1) Сначала вычерчивается поперечное сечение. Случайные оси х, у ставим так, чтобы все точки поперечного сечения находились в 1-м квадранте (рис.1). Каждому прокатному профилю присваивается порядковый номер. Наносим местные оси координат х_i, у_i, проходящие через известные центры тяжести i –го профиля. Оси х_i, у_iпараллельны случайным осям х, у соответственно.

2) Наносим на рисунок известные размеры сечения, взятые из задания или из соответствующих таблиц сортамента прокатной стали.

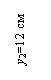
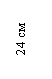
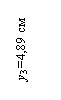
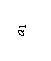
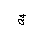
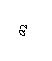
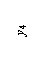
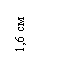
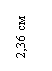
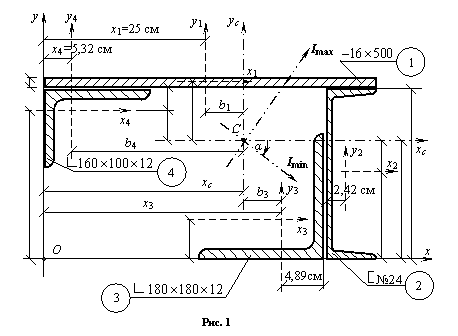
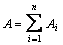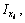
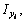
3) Вводим обозначения: х_i, у_i – абсцисса и ордината центра тяжести соответственно i– го профиля относительно случайных осей х, у; А_i – площадь сечения i– го профиля, – площадь поперечного сечения всего составного сечения; 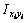– осевые и центробежные моменты инерции i –го профиля относительно местных осей х_i, у_i.

4) Следуя предложенной методике, выпишем геометрические характеристики для поперечного сечения, изображенного на рис. 1:

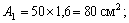
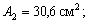
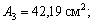
х ₁ = 25 см; х ₂ = 43,42 см; х ₃ = 36,11 см; х ₄ = 5,32 см;

у ₁ = 24,8 см; у ₂ = 12 см; у ₃ = 4,89 см; у ₄ = 21,64 см;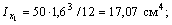

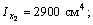
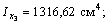
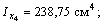
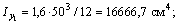
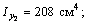
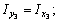
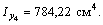
5) С помощью формул

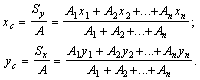
находим координаты центра тяжести всего поперечного сечения:

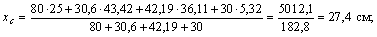
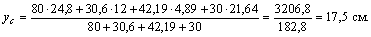
6) Наносим оси х_с, у_с, которые проходят через центр тяжести С всего составного поперечного сечения и определяем расстояния между осями х_с и х_i, а также между осями у_с и у_i:

а ₁ = у ₁ – у_с = 24,8 – 17,5 = 7,3 см; b ₁ = х ₁ – х_с = 25 – 27,4 = –2,4 см;

а ₂ = у ₂ – у_с = 12 – 17,5 = –5,5 см; b ₂ = х ₂ – х_с = 43,42 – 27,4 = 16,02 см;

а ₃ = у ₃ – у_с = 4,89 – 17,5 = –12,61 см; b ₃ = х ₃ – х_с = 36,11 – 27,4 = 8,71 см;

а ₄ = у ₄ – у_с = 21,64 – 17,5 = 4,14 см; b ₄ = х ₄ – х_с = 5,32 – 27,4 = –22,08 см.

7) Используя формулы 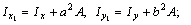получаем выражения для вычисления осевых моментов инерции относительно центральных осей х_с и у_с всего поперечного сечения:

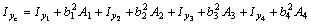
или окончательно:

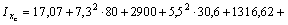
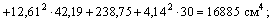
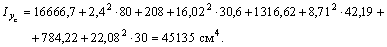
По формуле 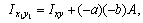находим значение центробежного момента инерции относительно осей х_с, у_с:

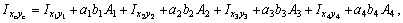
где, согласно рис. 1, имеем 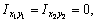так как швеллер и полоса имеют оси симметрии х₂ и х₁, у₁ соответственно.

Для вычисления 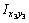для равнополочного уголка предварительно выпишем из таблицы сортамента «Уголки стальные горячекатаные равнополочные» 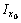= 2093 см⁴,= 540 см⁴,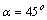, 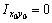(рис. 2, а).

Тогда формула 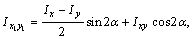принимает вид:

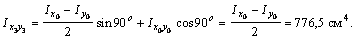
Для вычисления 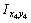для неравнополочного уголка (рис. 2, б) предварительно выпишем из таблицы сортамента

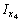= 238,75 см⁴, 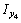= 784,22 см⁴, I _uv = 0, I _u = 142 см⁴, 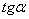= 0,388

и затем, согласно формуле получаем:

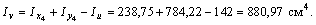
Таким образом, формула 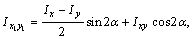для рассматриваемого случая принимает вид:

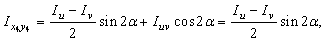
где 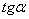= 0,388; = –21^о12^/ (рис.2, б), тогда

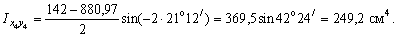
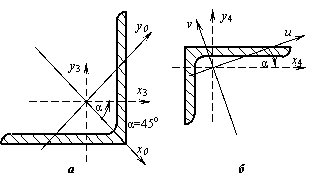
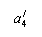
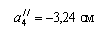
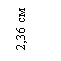
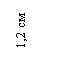
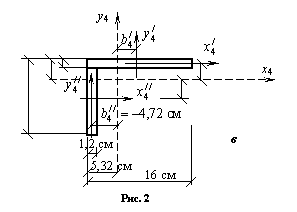
Значение центробежного момента 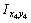можно вычислить, используя формулу 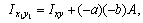. Для этого рассмотрим рис. 2, в. Разобьем уголок на два прямоугольника с

и .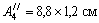

В этом случае по формуле 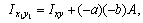получаем

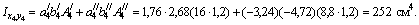
Как видно, результаты очень близки по значениям.

Теперь можно приступить к определению центробежного момента всего составного сечения относительно осей хс, ус:

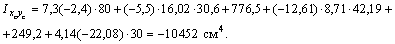
8) Главные оси инерции можно построить, повернув центральные оси х_с, у_с на угол (рис. 1):

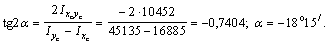
9) Величины главных моментов инерции определяем по формуле

Окончательно получаем, что I _max = 48582 см⁴, I _min = 13438 см⁴.

Полученные значения удовлетворяют условию :

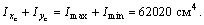
Таким образом, определены все геометрические характеристики сложного составного поперечного сечения, показанного на рис.1.

Определить положение главных центральных осей и вычислить главные центральные моменты инерции для сечения (см. рис.), состоящего из неравнобокого уголка №14/9 (ГОСТ 8510-57) и швеллера №24 (ГОСТ 8240-56).

Разбиваем фигуру на части, геометрические характеристики которых можно взять из таблиц сортамента, на швеллер и уголок; через их центр тяжести c₁ и c₂ проводим центральные оси z₁, y₁ и z₂, y₂, параллельные их сторонам. Поскольку z₁ - ось симметрии швеллера, то она и ось y₁ являются его главными центральными осями. Главная центральная ось уголка v-v образует с его центральной осью z₂ угол .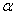

Из таблиц сортамента имеем:

Для швеллера №24 F₁= 30,6 см²

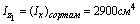
координаты центра тяжести

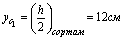
h= 24 см b= 9 см

Для уголка №14/9 F₂= 22,2 см²

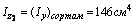
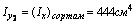
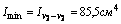
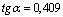
координаты центра тяжести

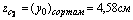
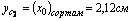
1) Определим координаты центра тяжести всего сечения, для этого принимаем за исходные оси главные центральные оси швеллера z₁ и y₁ и согласно (4.4) получаем:

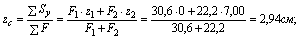
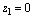
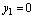
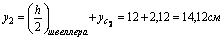
Через центр тяжести C проводим центральные оси z_c и y_c, параллельные проведенным ранее центральным осям швеллера и уголка.

Для проверки правильности определения координат центра тяжести, вычислим статические моменты относительно центральных осей z_c и y_c, которые должны быть равны нулю.

Получаем:

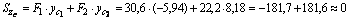
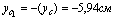
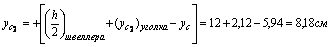
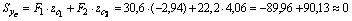
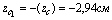
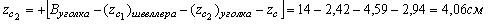
2) Вычислим осевые и центробежный моменты инерции всего сечения в системе центральных осей z_c, y_c по формулам:

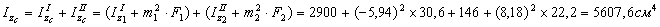
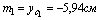
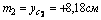
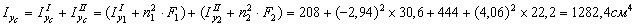
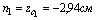
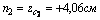
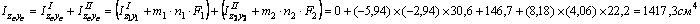
для швеллера 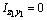, т.к. оси z₁ и y₂ являются для швеллера главными центральными; для уголка 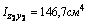согласно сортамента.

3) Определяем угол наклона главных центральных осей u и v относительно центральных осей z_c, y_c:

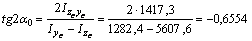
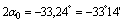
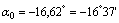
Поскольку угол 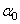отрицательный, он откладывается по ходу часовой стрелки, а т.к. 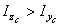, то поворотом оси z на угол, меньший 45°, мы получим направление главной центральной оси u, относительно которой главный момент инерции максимален I_u=I _max.

4) Главные моменты инерции определяем по формулам

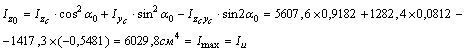
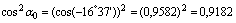
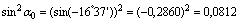
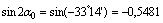
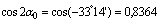
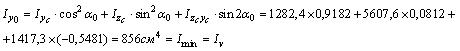
Проверки: а) Определяем центробежный момент инерции относительно главных центральных осей , который должен быть равен нулю:

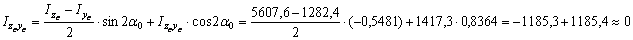
б) Определим главные центральные моменты инерции I_u и I_v по формулам:

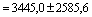
I_u=I _max = 3445,0 + 2585,6 = 6030,6 см⁴

I_v=I_min= 3445,0 - 2585,6 = 859,4 см⁴

Максимальное расхождение составляет:

.

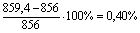в) Должно удовлетворяться условие:

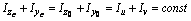
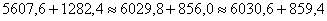
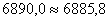
Расхождение составляет:

.

5. Определение моментов сопротивления сечения.

Наиболее удаленными точками от осей u и v являются точки A и B:

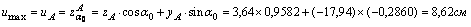
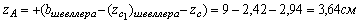
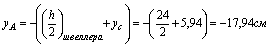
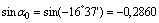
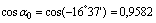
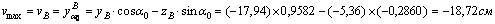
y_B = y_A = -17,94 см

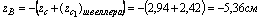
По формулам получаем:

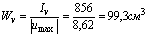
6. Радиусы инерции вычисляются по формулам (4.35), (4.36):

F = F₁ + F₂ = 30,6 +22,2 = 52,8 см²

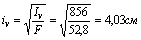
Откладывая отрезки i_u= 10,69см и i_v= 4,03см перпендикулярно соответствующим осям, строим на них, как на полуосях, эллипс инерции (см. рис.).

Дата добавления: 2013-12-13