Решение. 1) определить положение центра тяжести сечения;

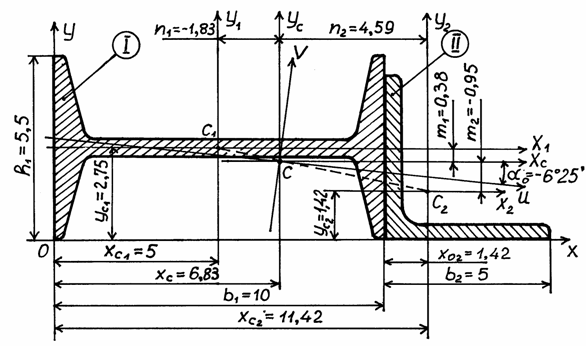
Рис.1

Пример 8.

Для поперечного сечения (см. рис.1), состоящего из двутавра №10 и равнобокого уголка 50х50х5 мм, требуется:

1) определить положение центра тяжести сечения;

2) найти центральные осевые и центробежный моменты инерции сечения;

3) определить направление главных центральных осей инерции сечения (U и V);

4) вычислить главные центральные моменты инерции сечения.

1. Выписываем из таблиц сортамента прокатных профилей необходимые для расчета данные:

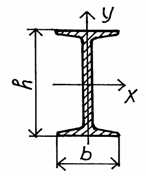
- Двутавр №10 (ГОСТ 8239-56);

A ₁ =12 см²; b =5,5 см; h =10 см; I _x= 198 см⁴; I _y1= 17,9 см⁴.

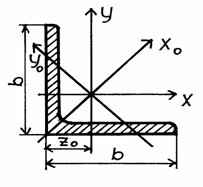
- Уголок равнобокий 50х50х5 (ГОСТ 8509-57);

A = 4,8 см²; b = 5 см; z₀= 1,42 см; I _x= 11,2 см⁴ ; I _x0= 17,8 см⁴ ; I _y0= 4,63 см⁴

2. Вычерчиваем в масштабе сечение. Для определения положения центра тяжести составного сечения обозначим двутавр – I и равнобокий уголок – II и проведем собственные центральные оси X ₁, Y ₁ и X ₂, Y ₂. Проводим вспомогательные оси X, Y. Тогда координаты центра тяжести сечений I и II относительно осей X, Y:

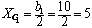см;

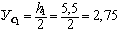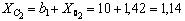см;

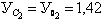см;

см.

Координаты центра тяжести всего сечения:

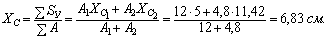
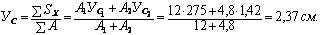
где А ₁ =12 см²; А ₂ =4,8 см² – площади поперечных сечений.

Наносим эти размеры на чертеж и через полученный центр тяжести С проводим центральные оси X _c и Y _c. Проверяем правильность вычислений: центр тяжести составного сечения должен лежать на линии, соединяющей центры тяжести первого и второго сечений.

3. Вычисляем центральные осевые и центробежный моменты инерции составного сечения. Воспользуемся формулами для определения моментов инерции при параллельном переносе осей:

; ;

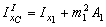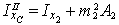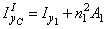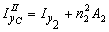; ; (1)

; .

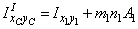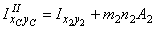где m ₁, m ₂ – расстояние между параллельными осями X ₁ и Х_С, X ₂ и Х_С соответственно;

n ₁, n ₂ – расстояние между параллельными осями Y ₁ и Y _c, Y ₂ и Y _c соответственно.

На основании данных чертежа получим:

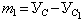= 2,75 – 2,37 = 0,38 см;

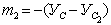= –(2,27 – 1,42) = –0,95 см;

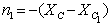= –(6,83 – 5) = –1,83 см;

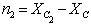= 11,42 – 6,83 = 4,59 см.

Вычисляем центральные осевые моменты инерции всего сечения, равные сумме моментов инерции фигур, составляющих это сечение, с учетом формулы (1):

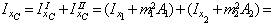
= (17,9 +0,38²×12) +(11,2 + (– 0,95)²×4,8) = 19,63 + 15,53 = 352 см⁴; (2)

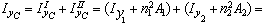
= (198 + (– 1,83)²×12) +(11,2 + 4,59²×4,8) = 238,2 + 111,9 = 350,1 см⁴. (3)

Центробежный момент инерции составного сечения вычисляем с учетом формул (1) аналогично:

=

= (0 + 0,38×(–1,83)×12) + (– 6,58 + (– 0,95)×4,59×4,8) = (– 8,34) + (– 27,5) = – 35,8 см⁴. (4)

В этой формуле для двутавра, являющегося симметричным сечением относительно собственных центральных осей, центробежный момент инерции 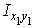= 0, т.к. эти оси - главные центральные оси двутавра. Для равнобокого уголка (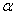= 45º):

;

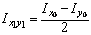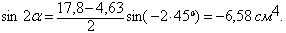
Дата добавления: 2013-12-13