Решение. Знак Ixy при различных положениях равнобоких и неравнобоких уголков выбирается согласно рисунок 2

Рис.1

Пример 9.

Рис.2

Знак I _xy при различных положениях равнобоких и неравнобоких уголков выбирается согласно рисунок 2. В нашем случае берется знак минус.

4. Определим направление главных центральных осей на основании вычислений по формулам (2), (3) и (4):

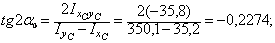
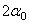= –12º48’; 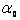= –6º24’.

Угол 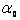< 0, поэтому угол 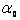= –6º24’ отложим от оси Х_С в направлении часовой стрелки и проведем главную ось U, а ей перпендикулярно – главную ось V (рис. 2).

5. Вычислим значения главных центральных моментов инерции

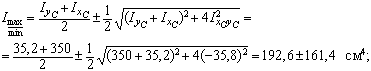
I _max = 354 см⁴ = 354·10^-8 м⁴;

I _min = 31,2 см⁴ = 31,2·10^-8 м⁴.

Положение оси U (I _min) легко определить, т.к. эта ось, во-первых, пересекает сечение по наибольшему протяжению и, во-вторых, располагается ближе к той центральной оси инерции (оси Х_С), относительно которой центральный момент инерции имеет меньшую величину, т.е. (I _xc< I _yc).

Таким образом I _V = I _min = 31,2·10^-8 м⁴,

I _U = I _max = 354 см⁴ = 354·10^-8 м⁴.

Проверка: ;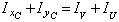

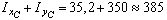см⁴;

см⁴.

Т.к. оси V и U главные, то должно выполняться условие равенства нулю центробежного момента инерции, вычисленного относительно главных осей V и U, т.е. 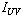= 0. Тогда при 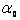= –6º25’ получим:

где ,

.

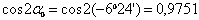Задано составное сечение, состоящее из двутавра № 20, неравнобокого уголка 100х63х6 мм и пластины 240х20 мм. На рис. 1 представлено это сечение.

Требуется:

1. Определить центр тяжести сечения.

2. Вычислить осевые и центробежные моменты инерции сечения относительно центральных осей.

3. Определить положение главных центральных осей инерции сечения.

4. Вычислить главные центральные моменты инерции сечения.

Вычерчиваем сечение в масштабе на листе чертежной или миллиметровой бумаги. Обозначим отдельные элементы: I - двутавр; II – пластина; III – неравнобокий уголок (рис. 2). Затем проводим центральные оси каждого сечения X₁, Y₁; X₂, Y₂ и X₃, Y₃.

Из сортамента выписываем все необходимые для расчета данные:

1. Двутавр №20 (ГОСТ 8239 – 89).

Как видим из чертежа (рис.2), двутавр расположен горизонтально, а в сортаменте – вертикально. По этой причине принимаем осевые моменты инерции 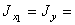115 см⁴, 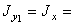1840 м⁴,

b ₁ = h = 20 см, h ₁ = b = 10 см, где J _x, J _y, h и b – числовые данные из сортамента. Площадь поперечного сечения А ₁ = 26,8 см².

2. Пластина (прямоугольник): b ₂ = 16 см; h ₂ = 2 см.

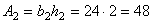см².

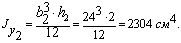
3. Уголок неравнобокий 100х63х6 мм (ГОСТ – 8510 – 86):

А ₃ = 9,58 см³; 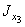= 98,3 см⁴; 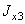= 30,6 см⁴; = 18,2 см⁴;

х ₀ = 1,42 см; у ₀ = 3,23 см; 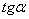= 0,393; b ₃ = 0,3 см; h ₃ = 10 см.

Дата добавления: 2013-12-13